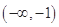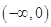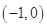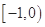题目内容
设函数f(x)=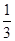 x-ln x(x>0),则y=f(x)( ).
x-ln x(x>0),则y=f(x)( ).
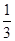 x-ln x(x>0),则y=f(x)( ).
x-ln x(x>0),则y=f(x)( ).A.在区间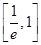 ,(1,e)内均有零点 ,(1,e)内均有零点 |
B.在区间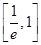 ,(1,e)内均无零点 ,(1,e)内均无零点 |
C.在区间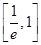 内有零点,在区间(1,e)内无零点 内有零点,在区间(1,e)内无零点 |
D.在区间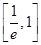 内无零点,在区间(1,e)内有零点 内无零点,在区间(1,e)内有零点 |
D
法一 因为f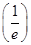 =
=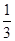 ·
·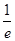 -ln
-ln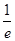 =
=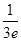 +1>0,f(1)=
+1>0,f(1)=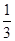 -ln 1=
-ln 1=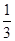 >0,f(e)=
>0,f(e)=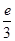 -ln e=
-ln e=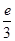 -1<0,∴f
-1<0,∴f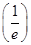 ·f(1)>0,f(1)·f(e)<0,故y=f(x)在区间
·f(1)>0,f(1)·f(e)<0,故y=f(x)在区间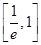 内无零点(f(x)在
内无零点(f(x)在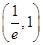 内根据其导函数判断可知单调递减),在区间(1,e)内有零点.
内根据其导函数判断可知单调递减),在区间(1,e)内有零点.
法二 在同一坐标系中分别画出y=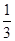 x与y=ln x的图象,如图所示.
x与y=ln x的图象,如图所示.
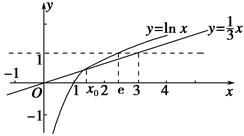
由图象知零点存在区间(1,e)内.
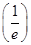 =
=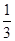 ·
·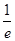 -ln
-ln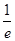 =
=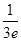 +1>0,f(1)=
+1>0,f(1)=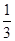 -ln 1=
-ln 1=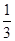 >0,f(e)=
>0,f(e)=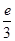 -ln e=
-ln e=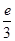 -1<0,∴f
-1<0,∴f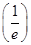 ·f(1)>0,f(1)·f(e)<0,故y=f(x)在区间
·f(1)>0,f(1)·f(e)<0,故y=f(x)在区间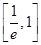 内无零点(f(x)在
内无零点(f(x)在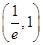 内根据其导函数判断可知单调递减),在区间(1,e)内有零点.
内根据其导函数判断可知单调递减),在区间(1,e)内有零点.法二 在同一坐标系中分别画出y=
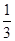 x与y=ln x的图象,如图所示.
x与y=ln x的图象,如图所示.
由图象知零点存在区间(1,e)内.

练习册系列答案
相关题目
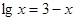 的近似解,可以取的一个区间是( )
的近似解,可以取的一个区间是( )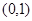


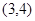
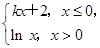 (k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
(k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )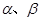 是一元二次方程
是一元二次方程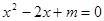 的两个虚根.若
的两个虚根.若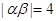 ,则实数
,则实数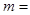 .
.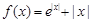 ,若关于
,若关于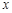 的方程
的方程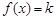 有两个不同的实根,则实数
有两个不同的实根,则实数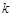 的取值范围是( )
的取值范围是( )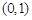
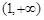

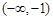
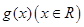 的图像如图所示,关于
的图像如图所示,关于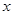 的方程
的方程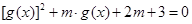 有三个不同的实数解,则
有三个不同的实数解,则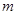 的取值范围是_______________.
的取值范围是_______________.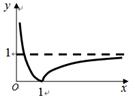
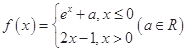 ,若函数
,若函数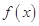 在
在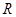 上有两个零点,则
上有两个零点,则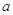 的取值范围是
的取值范围是