题目内容
已知y=f(x)与y=g(x)都为R上的可导函数,且f'(x)>g'(x),则下面不等式正确的是
- A.f(2)+g(1)>f(1)+g(2)
- B.f(1)+f(2)>g(1)+g(2)
- C.f(1)-f(2)>g(1)-g(2)
- D.f(2)-g(1)>f(1)-g(2)
A
分析:先根据导数的运算法则将f′(x)>g′(x)转化为[f(x)-g(x)]′>0,然后由函数的导数与单调性的关系,得出函数f(x)-g(x)在R上为增函数,分别令x=1,2得出大小关系式.
解答:∵f'(x)>g'(x),∴f'(x)-g'(x)>0,∴[f(x)-g(x)]′>0,∴函数f(x)-g(x)在R上为增函数.
∵1<2,∴f(1)-g(1)<f(2)-g(2),移向即得f(2)+g(1)>f(1)+g(2)
故选A
点评:本题主要考查导数的运算法则,函数的导数与单调性的关系.本题关键是将f'(x)>g'(x),移向,得出函数f(x)-g(x)在R上为增函数.
分析:先根据导数的运算法则将f′(x)>g′(x)转化为[f(x)-g(x)]′>0,然后由函数的导数与单调性的关系,得出函数f(x)-g(x)在R上为增函数,分别令x=1,2得出大小关系式.
解答:∵f'(x)>g'(x),∴f'(x)-g'(x)>0,∴[f(x)-g(x)]′>0,∴函数f(x)-g(x)在R上为增函数.
∵1<2,∴f(1)-g(1)<f(2)-g(2),移向即得f(2)+g(1)>f(1)+g(2)
故选A
点评:本题主要考查导数的运算法则,函数的导数与单调性的关系.本题关键是将f'(x)>g'(x),移向,得出函数f(x)-g(x)在R上为增函数.

练习册系列答案
相关题目
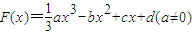 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B. ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.