题目内容
已知数列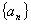 满足
满足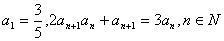 .
.
(1)求证:数列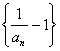 为等比数列;
为等比数列;
(2)是否存在互不相等的正整数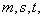 使
使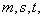 成等差数列,且
成等差数列,且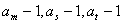 , 成等比数列?如果存在,求出所有符合条件的
, 成等比数列?如果存在,求出所有符合条件的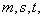 ,;如果不存在,请说明理由.
,;如果不存在,请说明理由.
解析:因为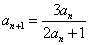 ,所以
,所以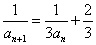 .所以
.所以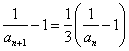 .
.
因为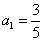 ,则
,则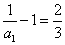 .所以数列
.所以数列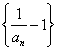 是首项为
是首项为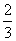 ,公比为
,公比为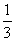 的等比数列.
的等比数列.
(2)由(1)知,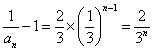 ,所以
,所以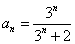 .-
.-
假设存在互不相等的正整数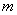 ,
,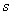 ,
,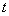 满足条件,
满足条件,
则有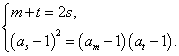 由
由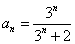 与
与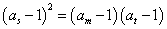 ,
,
得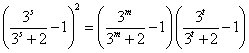 .
.
即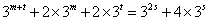 .因为
.因为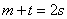 ,所以
,所以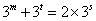 .
.
因为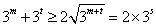 ,当且仅当
,当且仅当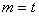 时等号成立,
时等号成立,
这与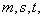 互不相等矛盾.所以不存在互不相等的正整数
互不相等矛盾.所以不存在互不相等的正整数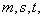 满足条件.
满足条件.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 B.
B.
 D.
D.
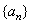 的前n项和为
的前n项和为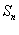 ,若
,若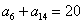 ,则
,则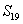 =______________.
=______________.  (m∈R,i为虚数单位)在复平面上对应的点不可能位于 ( )
(m∈R,i为虚数单位)在复平面上对应的点不可能位于 ( )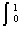
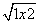 dx,对任意x∈R,不等式a(cos2x-m)+πcos x≥0恒成立,则实数m的取值范围为_
dx,对任意x∈R,不等式a(cos2x-m)+πcos x≥0恒成立,则实数m的取值范围为_  ,则
,则
 B.
B.  C.
C.  D. 2
D. 2 的焦点为
的焦点为 ,
, 是C上一点,
是C上一点, ,则
,则 ( )
( ) ,
, 的定义域都为R,且
的定义域都为R,且 .
. .|
.| .
. .|
.| 是虚数单位,复数
是虚数单位,复数 ( )
( ) B.
B.  D.
D. 