Question

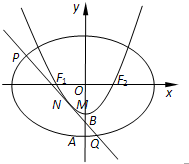设椭圆C₁：

x2

5

+

y2

4

=1的左、右焦点分别是F₁、F₂，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C₂：y=mx²-n（m＞0，n＞0）与y轴的交点为B，且经过F₁，F₂点．
（Ⅰ）求抛物线C₂的方程；
（Ⅱ）设M（0，-

4

5

），N为抛物线C₂上的一动点，过点N作抛物线C₂的切线交椭圆C₁于P、Q两点，求△MPQ面积的最大值．

Answer 1

分析：（1）由题设条件知n=1，再由F₁（-1，0），F₂（1，0），故m=1，由此可求出抛物线C₂的方程．
（2）先写出直线PQ的方程，代入椭圆方程整理得关于x的一元二次方程．然后利用根与系数的关系结合题设条件进行求解．最后利用求函数最值的方法即可求得△MPQ面积的最大值．

解答：解：（1）由题意可知B（0，-1），则A（0，-2），故n=1．
又F₁（-1，0），F₂（1，0），故m=1．
所以抛物线C₂的方程为：y=x²-1（15分）
（2）设N（t，t²-1），
由于y'=2x知直线PQ的方程为：y-（t²-1）=2t（x-t）．
即y=2tx-t²-1．（7分）
代入椭圆方程整理得：4（1+5t²）x²-20t（t²+1）x+5（t²+1）²-20=0，
△=400t²（t²+1）²-80（1+5t²）[（t²+1）²-4]=80（-t⁴+18t²+3），x1+x2=

5t(t2+1)

1+5t2

，x1x2=

5(t2+1)2-20

4(1+5t2)

，
故|PQ|=

1+4t2

|x1-x2|=

1+4t2

.

(x1+x2)2-4x1x2

=

5 • 1+4t2 • -t4+18t2+3

1+5t2

．（10分）
设点M到直线PQ的距离为d，
则d=

|+ 4 5 -t2-1|

1+4t2

=

|t2+ 1 5 |

1+4t2

．（12分）
所以，△MPQ的面积
S=

1

2

|PQ|•d=

1

2

5 • 1+4t2 • -t4+18t2+3

1+5t2

•

t2+ 1 5

1+4t2

=

5

10

-t4+18t2+3

=

5

10

-(t2-9)2+84

≤

5

10

84

=

105

5

（14分）
当t=±3时取到“=”，经检验此时△＞0，满足题意．
综上可知，△MPQ的面积的最大值为

105

5

．（15分）

点评：本题考查圆锥曲线和直线的位置关系和综合应用，解题时要认真审题，注意韦达定理的合理运用．