题目内容
已知矩形
的顶点都在半径为4的球
的球面上，且
，
，则棱锥
的体积为（ ）
A． | B． | C． | D． |
A
解析试题分析：棱锥中顶点在底面的射影
是矩形的中心,
体积为
考点：椎体的体积
点评：结合球的有关知识可知椎体的侧棱为球的半径，顶点在底面的射影为矩形中心，因此求出椎体的高，代入体积公式求解
练习册系列答案
相关题目
已知一个圆柱的底面直径与高都等于一个球的直径，则球的表面积等于圆柱表面积的（ ）倍
| A．1 | B． | C． | D． |
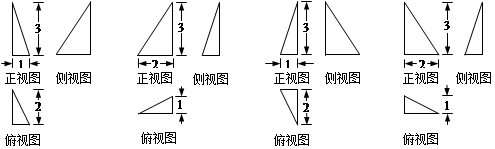
如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为
| A．三棱台、三棱柱、圆锥、圆台 | B．三棱台、三棱锥、圆锥、圆台 |
| C．三棱柱、正四棱锥、圆锥、圆台 | D．三棱柱、三棱台、圆锥、圆台 |
棱长都是1的三棱锥的表面积为（ ）
A． | B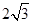． | C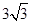． | D． |
如图是水平放置的平面图形的斜二测直观图，其原来平面图形面积是（ ）
A．2 | B．4 | C．4 | D．8 |
