题目内容
(本小题满分13分)
已知椭圆 的一个焦点和抛物线
的一个焦点和抛物线 的焦点相同,过椭圆右焦点F且垂直
的焦点相同,过椭圆右焦点F且垂直 轴的弦长为2.
轴的弦长为2.
(I)求椭圆C的方程;
(II)若与直线 相垂直的直线
相垂直的直线 与椭圆C交于B、D两点,求
与椭圆C交于B、D两点,求 的最大值.
的最大值.
(Ⅰ) ; (Ⅱ)
; (Ⅱ)
【解析】
试题分析:(I)根据抛物线和椭圆的性质即可求出椭圆的方程为 ;(Ⅱ).根据题意,设
;(Ⅱ).根据题意,设 方程为
方程为 ,设
,设 与椭圆
与椭圆 交于点
交于点 ,
,
联立方程 ,得
,得 .
.  ,解得
,解得 ,由韦达定理得
,由韦达定理得 ,可得
,可得 ,又因为点O到直线
,又因为点O到直线 的距离
的距离 所以
所以 ,即可求的
,即可求的 面积的最大值为
面积的最大值为 .
.
试题解析:【解析】
(I)因为抛物线 的焦点坐标为
的焦点坐标为 ,
,
把直线 代人椭圆方程
代人椭圆方程 ,得
,得 ,
, ,
,
即 ,即
,即 ,得
,得 ,
,
∴椭圆方程为 ,
,
(Ⅱ). ,可设
,可设 方程为
方程为 ,
,
设 与椭圆
与椭圆 交于点
交于点 ,
,
联立方程 ,得
,得 .
.
 ,解得
,解得 ,
,
由韦达定理得

又因为点O到直线 的距离
的距离
所以
(当且仅当 ,即
,即 时取到最大值)
时取到最大值)
经验证 满足
满足 ,
,
所以 面积的最大值为
面积的最大值为 .
.
考点:1.椭圆的标准方程和性质;2 .直线与椭圆的位置关系.

练习册系列答案
相关题目
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则无穷数列
,则无穷数列 前
前 项和的极限为 .
项和的极限为 .  的倾斜角
的倾斜角 .
.  的定义域为D,若任取
的定义域为D,若任取 ,存在唯一的
,存在唯一的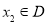 满足
满足 ,则称C为函数
,则称C为函数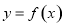 在D上的均值.给出下列五个函数:
在D上的均值.给出下列五个函数: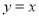 ;②
;② ;③
;③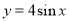 ;④
;④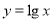 ;⑤
;⑤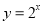 .则所有满足在其定义域上的均值为2的函数的序号为_________.
.则所有满足在其定义域上的均值为2的函数的序号为_________. ,则输出的
,则输出的 ( )
( )
 B.
B.  C.
C.  D.
D. 
 的直线与圆
的直线与圆 有公共点,则该直线的倾斜角的取值范围是
有公共点,则该直线的倾斜角的取值范围是 B.
B.  C.
C.  D.
D. 

 D.
D. 