题目内容
如图,V是边长为a的等边△ABC所在平面外一点,且VA=VB=VC=a,E、F分别为VA、BC的中点,?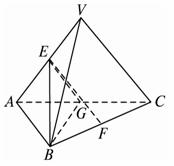
(1)求证:EF是VA与BC的公垂线;
(2)求VA与BC的距离;
(3)求VC与BE所成角的大小;
(4)VF与BE所成角的大小.
解析:(1)连结VF、AF.?
∵△ABC≌△VBC,∴AF=VF.?
又E 为VA的中点,?
∴EF⊥VA.?
同理可得EF⊥BC.?
∴EF是VA与BC的公垂线.?
(2)∵EF是VA与BC的公垂线,?
∴EF的长即为VA与BC的距离.?
由所有的棱长均为a,求得AF=VF=![]() .?
.?
进而可得EF =![]() . ∴VA与BC的距离为
. ∴VA与BC的距离为![]() .?
.?
(3)∵E为VA的中点,?
∴取AC的中点G,连结EG、BG.则EG∥VC.?
∴∠BEG或其补角即为VC与BE所成的角.?

在△BEG中,BE=BG=![]() ,EG=
,EG=![]() .?
.?
由余弦定理可得 cos∠BEG=![]() .?
.?
∴VC与BE所成的角为arccos![]() .?
.?
(4)∵E为VA的中点,?
∴取AF的中点M,连结EM、BM,则EM∥VF.?
∴∠BEM或其补角即为VF与BE所成的角.?
在△BEM中,BE=![]() ,EM=
,EM=![]() .?
.?
而BM=MF2+BF2=![]() .?
.?
由余弦定理得cos∠BEM =![]() .?
.?
∴VF与BE所成的角为arccos![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
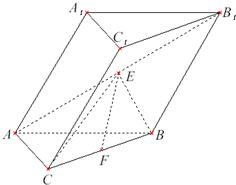 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点. 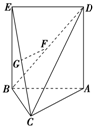 如图△ABC中,AC=BC=
如图△ABC中,AC=BC=
