题目内容
已知抛物线的焦点在直线l：x-2y-4=0上，求抛物线的标准方程．
解：令x=0得y=-2；令y=0得x=4；
∴抛物线的焦点坐标为：（4，0），（0，-2）--------------------------------------------------（4分）
当焦点为（4，0）时，即
=4，
∴p=8，此时抛物线方程为：y2=16x；--------------（7分）
当焦点为（0，-2）时，即=2，
∴p=4，此时抛物线方程为：x2=-8y；
故所求抛物线的标准方程为：y2=16x 或x2=-8y；-----------------------------（10分）
分析：分焦点在x轴和y轴两种情况分别求出焦点坐标，然后根据抛物线的标准形式可得答案．
点评：本题主要考查抛物线的标准方程．解题时注意分焦点在x轴上、焦点在y轴上两种情形讨论，属基础题．
∴抛物线的焦点坐标为：（4，0），（0，-2）--------------------------------------------------（4分）
当焦点为（4，0）时，即
=4，∴p=8，此时抛物线方程为：y2=16x；--------------（7分）
当焦点为（0，-2）时，即
=2，∴p=4，此时抛物线方程为：x2=-8y；
故所求抛物线的标准方程为：y2=16x 或x2=-8y；-----------------------------（10分）
分析：分焦点在x轴和y轴两种情况分别求出焦点坐标，然后根据抛物线的标准形式可得答案．
点评：本题主要考查抛物线的标准方程．解题时注意分焦点在x轴上、焦点在y轴上两种情形讨论，属基础题．
练习册系列答案
相关题目
一青蛙从点A0（x0，y0）开始依次水平向右和竖直向上跳动，其落点坐标依次是Ai（xi，yi）（i∈N*），（如图所示，A0（x0，y0）坐标以已知条件为准），Sn表示青蛙从点A0到点An所经过的路程．
开始依次水平向右和竖直向上跳动，其落点坐标依次是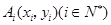
，(如图所示，
坐标以已知条件为准)，
表示青蛙从点
到点
所经过的路程。
准线上
，
均在该抛物线上，并且直线
.
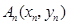要么落在
所表示的曲线上，
所表示的曲线上，并且
,
（不需证明）；
所表示的曲线上，要么落在
所表示的曲线上，并且
，求
已知抛物线C的顶点在原点, 焦点为F(0, 1).
，抛物E与直ly=k（x+1）（k∈R）相交于A、B两点．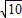
时，求k的值．