题目内容
(本题满分18分,其中第1小题4分,第2小题6分,第,3小题8分)
一青蛙从点 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是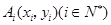 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
(1) 若点 为抛物线
为抛物线
 准线上
准线上
一点,点 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线
 经
经
过该抛物线的焦点,证明 .
.
(2)若点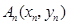 要么落在
要么落在 所表示的曲线上,
所表示的曲线上,
要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,
,
试写出 (不需证明);
(不需证明);
(3)若点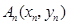 要么落在
要么落在 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求 的表达式.
的表达式.

解:(1)设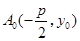 ,由于青蛙依次向右向上跳动,
,由于青蛙依次向右向上跳动,
所以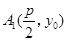 ,
,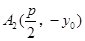 ,由抛物线定义知:
,由抛物线定义知: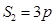

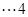 分
分
(2) 依题意,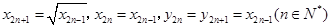
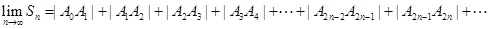
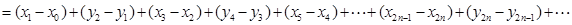
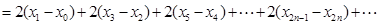
随着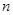 的增大,点
的增大,点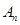 无限接近点
无限接近点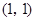
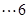 分
分
横向路程之和无限接近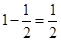 ,纵向路程之和无限接近
,纵向路程之和无限接近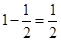
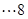 分
分
所以
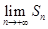 =
=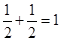
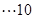 分
分
(3)方法一:设点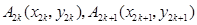 ,由题意,
,由题意,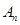 的坐标满足如下递推关系:
的坐标满足如下递推关系: ,且
,且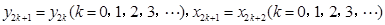
其中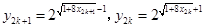
 分
分
∴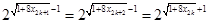 ,即
,即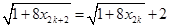 ,
,
∴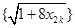 是以
是以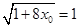 为首项,
为首项,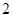 为公差的等差数列,
为公差的等差数列,
∴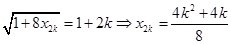 ,
,
所以当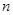 为偶数时,
为偶数时,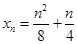 ,于是
,于是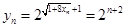 ,
,
又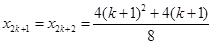
∴当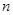 为奇数时,
为奇数时,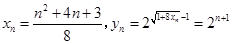
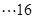 分
分
当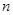 为偶数时,
为偶数时,

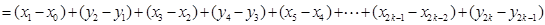
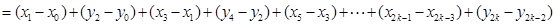

当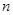 为奇数时,
为奇数时,
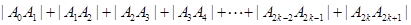
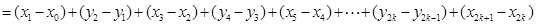
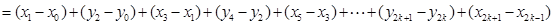
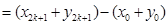
所以,当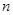 为偶数时,
为偶数时,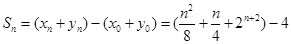
当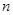 为奇数时,
为奇数时,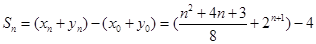
所以,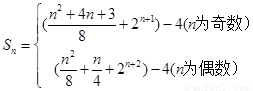
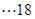 分
分
方法二:由题意知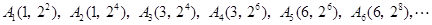
其中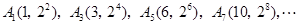
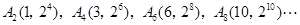
观察规律可知:下标为奇数的点的纵坐标为首项为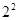 ,公比为
,公比为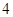 的等比数列。相邻横坐标之差为首项为2,公差为1的等差数列。下标为偶数的点也有此规律。并由数学归纳法可以证明。
的等比数列。相邻横坐标之差为首项为2,公差为1的等差数列。下标为偶数的点也有此规律。并由数学归纳法可以证明。
 分
分
所以,当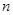 为偶数时,
为偶数时,

当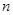 为奇数时,
为奇数时,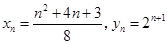
当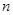 为偶数时,
为偶数时,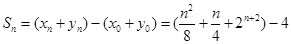
当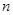 为奇数时,
为奇数时,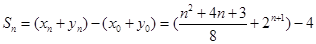
 分
分
所以,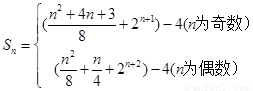
 分
分
【解析】略

 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点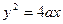 (
(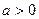 且
且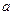 为常数),
为常数),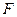 为其焦点.
为其焦点.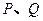 两点,且
两点,且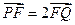 ,求直线
,求直线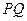 的斜率;
的斜率;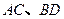 是过抛物线焦点
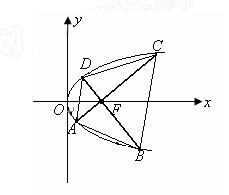
是过抛物线焦点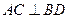 ,如图所示.求四边形
,如图所示.求四边形 面积的最小值
面积的最小值 .
.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
. 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; 上一点
上一点 经变换公式
经变换公式 与点
与点