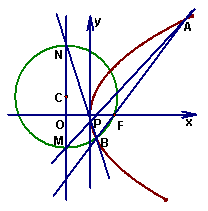
题目内容
已知抛物线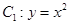 ,
,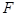 为抛物线的焦点,椭圆
为抛物线的焦点,椭圆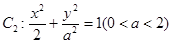 ;
;
(1)若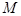 是
是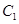 与
与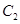 在第一象限的交点,且
在第一象限的交点,且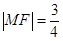 ,求实数
,求实数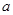 的值;
的值;
(2)设直线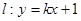 与抛物线
与抛物线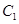 交于
交于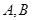 两个不同的点,
两个不同的点,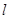 与椭圆
与椭圆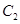 交于
交于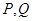 两个
两个
不同点,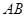 中点为
中点为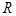 ,
,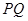 中点为
中点为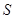 ,若
,若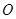 在以
在以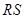 为直径的圆上,且
为直径的圆上,且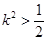 ,求实数
,求实数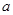
的取值范围.
【答案】
(1)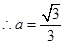 (2)
(2)
【解析】
试题分析:(1)设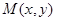 ,
, ,代入
,代入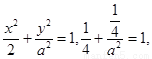
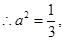 又
又 ,
,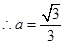
(2)设
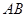 中点
中点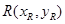 ,联立
,联立 ,得到
,得到 ,
,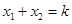 ,
,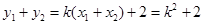 ,
,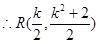
设 中点
中点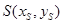 ,联立
,联立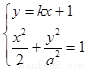 ,
, ,
,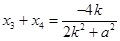 ,
,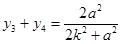 ,
,
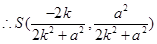 ,由条件知,
,由条件知, ,
,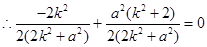 ,
,
 ,
,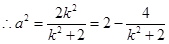 ,
,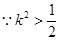 ,
,
 ,
,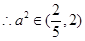 ,又
,又 ,
, ,又
,又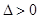 ,得到
,得到
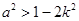 恒成立
恒成立
考点:直线与椭圆的位置关系
点评:解决的关键是能理解椭圆的性质,以及结合联立方程组的代数法思想来求解垂直时满足的条件,结合函数的知识得到范围。属于中档题。

练习册系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).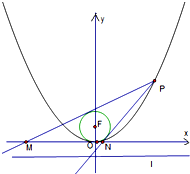 已知抛物线C:x2=2py(p>0)的焦点为
已知抛物线C:x2=2py(p>0)的焦点为