题目内容
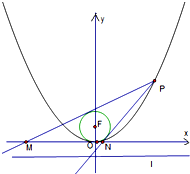 已知抛物线C:x2=2py(p>0)的焦点为F(0,
已知抛物线C:x2=2py(p>0)的焦点为F(0,| p |
| 2 |
| 3 |
| 2 |
(Ⅰ)求抛物线C的方程;
(Ⅱ)若圆F的方程为x2+(y-1)2=1,过点P作圆F的2条切线分别交x轴于点M,N,求△PMN面积的最小值及此事y0的值.
分析:(Ⅰ)由题意得出圆心的纵坐标为
,由圆心到准线的距离等于
求出p的值,则抛物线方程可求;
(Ⅱ)设出过P点的切线方程,由圆心F到切线的距离等于1整理得到关于切线斜率k的一元二次方程,方程的两个根为两条切线的斜率,由根与系数关系得到两根的和与积(用P点的坐标表示),单独写出两切线的方程,求出M和N的坐标,由数轴上的两点间的距离公式写出M、N的距离,把根与系数关系代入后化为P点纵坐标的表达式,则三角形PMN的面积化为了关于P点纵坐标的函数关系式,通过求导得到面积的最小值.
| p |
| 4 |
| 3 |
| 2 |
(Ⅱ)设出过P点的切线方程,由圆心F到切线的距离等于1整理得到关于切线斜率k的一元二次方程,方程的两个根为两条切线的斜率,由根与系数关系得到两根的和与积(用P点的坐标表示),单独写出两切线的方程,求出M和N的坐标,由数轴上的两点间的距离公式写出M、N的距离,把根与系数关系代入后化为P点纵坐标的表达式,则三角形PMN的面积化为了关于P点纵坐标的函数关系式,通过求导得到面积的最小值.
解答:解:(I)△FOP的外接圆的圆心在线段OF,FP的中垂线的交点上,且线段OF的中垂线为直线y=
,
则圆心的纵坐标为
,故圆心到准线的距离为
+
=
,解得p=2,即抛物线C的方程为x2=4y.
(II)由题意知过点P的圆x2+(y-1)2=1的切线的斜率存在,设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0.
则点F(0,1)到直线的距离d=
.令d=1,则
=1,
整理得(
-1)k2-2x0(y0-1)k+
-2y0=0.
设两条切线PM,PN的斜率分别为k1,k2,则k1+k2=
,k1k2=
,
且直线PM:y-y0=k1(x-x0),直线PN:y-y0=k2(x-x0),故M(x0-
,0),N(x0-
,0).
因此|MN|=|
-
|=y0|
|=y0
=
.
所以S△PMN=
|MN|y0=
.
设f(t)=
(t>2),则f′(t)=
,
令t2-3t-6=0,则t=
(舍),或t=
.
当t∈(2,
)时,f′(t)<0,f(t)在(2,
)上单点递减,
当t∈(
,+∞)时,f′(t)>0,f(t)在(
,+∞)上单调递增,
因此fmin(t)=f(
)=
=
(54+10
).
所以△PMN面积的最小值为
=
.
此时y0=
.
| p |
| 4 |
则圆心的纵坐标为
| p |
| 4 |
| p |
| 2 |
| p |
| 4 |
| 3 |
| 2 |
(II)由题意知过点P的圆x2+(y-1)2=1的切线的斜率存在,设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0.
则点F(0,1)到直线的距离d=
| |y0-kx-1| | ||
|
| |y0-kx0-1| | ||
|
整理得(
| x | 2 0 |
| y | 2 0 |
设两条切线PM,PN的斜率分别为k1,k2,则k1+k2=
| 2x0(y0-1) | ||
|
| ||
|
且直线PM:y-y0=k1(x-x0),直线PN:y-y0=k2(x-x0),故M(x0-
| y0 |
| k1 |
| y0 |
| k2 |
因此|MN|=|
| y0 |
| k2 |
| y0 |
| k1 |
| k1-k2 |
| k1k2 |
|
|
所以S△PMN=
| 1 |
| 2 |
|
设f(t)=
| t2(2t+t2) |
| (t-2)2 |
| 2t2(t2-3t-6) |
| (t-2)3 |
令t2-3t-6=0,则t=
3-
| ||
| 2 |
3+
| ||
| 2 |
当t∈(2,
3+
| ||
| 2 |
3+
| ||
| 2 |
当t∈(
3+
| ||
| 2 |
3+
| ||
| 2 |
因此fmin(t)=f(
3+
| ||
| 2 |
(
| ||||||||||||
(
|
=
(36+4
| ||
| 642 |
| 33 |
所以△PMN面积的最小值为
|
9+
| ||
| 16 |
54+10
|
此时y0=
3+
| ||
| 2 |
点评:本题考查了抛物线的标准方程,考查了直线与圆锥曲线的关系,考查了方程思想和函数思想,训练了利用导数求函数的最值,训练了学生的计算能力,繁杂的运算量会使学生对该题失去信心.此题属难题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目