题目内容
已知椭圆 的左、右焦点分别为F1、F2,左顶点为A,O为坐标原点.
的左、右焦点分别为F1、F2,左顶点为A,O为坐标原点.
若 .
.
(I)求椭圆C的方程;
(II)设过点F1的直线l交椭圆C于M、N两点,求 的取值范围.
的取值范围.
解:(I)由 得
得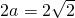 ,∴
,∴
由 得
得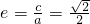 ,∴c=1,∴b=1
,∴c=1,∴b=1
∴椭圆C的方程为 ;
;
(II)由(I)知F1(-1,0),F2(1,0),则斜率不存在时,
 ,于是
,于是
∴
斜率存在时,设直线MN的方程为y=k(x+1),代入椭圆方程 ,消去y得
,消去y得
(1+2k2)x2+4k2x+2(k2-1)=0
设M(x1,y1),N(x2,y2),则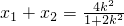

∵ ,
,
∴
∵1+2k2≥1,∴
∴
综上知,
分析:(I)由 ,根据椭圆的定义可得
,根据椭圆的定义可得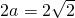 ,由
,由 ,根据离心率的定义得
,根据离心率的定义得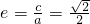 ,所以c=1,所以b=1,从而可求椭圆C的方程;
,所以c=1,所以b=1,从而可求椭圆C的方程;
(II)由(I)知F1(-1,0),F2(1,0),则斜率不存在时,用坐标分别表示出 ,从而利用数量积公式可求
,从而利用数量积公式可求
斜率存在时,设直线MN的方程为y=k(x+1),代入椭圆方程 ,消去y得
,消去y得
(1+2k2)x2+4k2x+2(k2-1)=0设M(x1,y1),N(x2,y2),则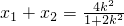
 用坐标分别表示出
用坐标分别表示出 ,
, 从而利用数量积公式可求
从而利用数量积公式可求 的范围.
的范围.
点评:本题以向量为载体,考查椭圆的标准方程,考查向量的数量积,解题时应注意分类讨论,同时正确用坐标表示向量.
 得
得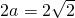 ,∴
,∴
由
 得
得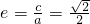 ,∴c=1,∴b=1
,∴c=1,∴b=1∴椭圆C的方程为
 ;
;(II)由(I)知F1(-1,0),F2(1,0),则斜率不存在时,
 ,于是
,于是
∴

斜率存在时,设直线MN的方程为y=k(x+1),代入椭圆方程
 ,消去y得
,消去y得(1+2k2)x2+4k2x+2(k2-1)=0
设M(x1,y1),N(x2,y2),则
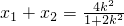

∵
 ,
,
∴

∵1+2k2≥1,∴

∴

综上知,

分析:(I)由
 ,根据椭圆的定义可得
,根据椭圆的定义可得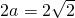 ,由
,由 ,根据离心率的定义得
,根据离心率的定义得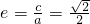 ,所以c=1,所以b=1,从而可求椭圆C的方程;
,所以c=1,所以b=1,从而可求椭圆C的方程;(II)由(I)知F1(-1,0),F2(1,0),则斜率不存在时,用坐标分别表示出
 ,从而利用数量积公式可求
,从而利用数量积公式可求
斜率存在时,设直线MN的方程为y=k(x+1),代入椭圆方程
 ,消去y得
,消去y得(1+2k2)x2+4k2x+2(k2-1)=0设M(x1,y1),N(x2,y2),则
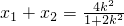
 用坐标分别表示出
用坐标分别表示出 ,
, 从而利用数量积公式可求
从而利用数量积公式可求 的范围.
的范围.点评:本题以向量为载体,考查椭圆的标准方程,考查向量的数量积,解题时应注意分类讨论,同时正确用坐标表示向量.

练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线