题目内容
函数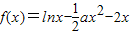 存在单调递减区间,则a的范围 .
存在单调递减区间,则a的范围 .
【答案】分析:根据函数的解析式可求得函数的定义域,求导,由函数 存在单调递减区间,转化为导数小于零在(0,+∞)有解,然后采用分离参数即可求得a的范围.
存在单调递减区间,转化为导数小于零在(0,+∞)有解,然后采用分离参数即可求得a的范围.
解答:解:∵函数 的定义域为(0,+∞),
的定义域为(0,+∞),
且函数 存在单调递减区间
存在单调递减区间
∴ =
= <0在(0,+∞)有解,
<0在(0,+∞)有解,
即-ax2-2x+1<0在(0,+∞)有解,
故a> 在(0,+∞)有解,
在(0,+∞)有解,
∴a>-1,
故a的范围为(-1,+∞).
故答案为:(-1,+∞)
点评:本题考查利用导数研究函数的单调性,根据题意,转化为导数小于零在(0,+∞)有解,是解题的关键,分离参数法简化运算,考查运算能力,属中档题.
 存在单调递减区间,转化为导数小于零在(0,+∞)有解,然后采用分离参数即可求得a的范围.
存在单调递减区间,转化为导数小于零在(0,+∞)有解,然后采用分离参数即可求得a的范围.解答:解:∵函数
 的定义域为(0,+∞),
的定义域为(0,+∞),且函数
 存在单调递减区间
存在单调递减区间∴
 =
= <0在(0,+∞)有解,
<0在(0,+∞)有解,即-ax2-2x+1<0在(0,+∞)有解,
故a>
 在(0,+∞)有解,
在(0,+∞)有解,∴a>-1,
故a的范围为(-1,+∞).
故答案为:(-1,+∞)
点评:本题考查利用导数研究函数的单调性,根据题意,转化为导数小于零在(0,+∞)有解,是解题的关键,分离参数法简化运算,考查运算能力,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 存在单调递减区间,则a的范围 .
存在单调递减区间,则a的范围 . 存在单调递减区间,则实数
存在单调递减区间,则实数 的取值
的取值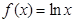 ,
,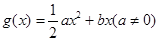 .
.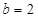 ,且函数
,且函数 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;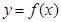 的图象
的图象 与函数
与函数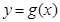 的图象
的图象 交于点
交于点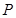 、
、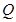 ,过线段
,过线段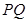 的中点作
的中点作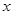 轴的垂线分别交
轴的垂线分别交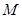 、
、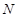 ,试判断
,试判断
 存在单调递减区间,求a的取值范围
存在单调递减区间,求a的取值范围