题目内容
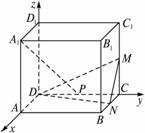
已知M、N、P分别是正方体ABCD—A1B1C1D1的棱CC1、BC、CD的中点.求证:A1P⊥平面DMN.
证明:建立如图所示的空间直角坐标系,设正方体的棱长为2,则D(0,0,0)、A1(2,0,2)、P(0,1,0)、M(0,2,1)、N(1,2,0).
∴向量![]() =(0,1,0)-(2,0,2)=(-2,1,-2),
=(0,1,0)-(2,0,2)=(-2,1,-2),
?![]() =(1,2,0),
=(1,2,0),![]() =(0,2,1).
=(0,2,1).
∴![]() ·
·![]() =(-2,1,-2)·(0,2,1)
=(-2,1,-2)·(0,2,1)
=(-2)×0+1×2+(-2)×1=0,?
![]() ·
·![]() ?=(-2,1,-2)·(1,2,0)
?=(-2,1,-2)·(1,2,0)
=(-2)×1+1×2+(-2)×0=0.
∴![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() .
.
∴A1P⊥![]() ,A1P⊥
,A1P⊥![]() .
.
又∵DM∩DN=D,
∴A1P⊥平面DMN.

练习册系列答案
相关题目
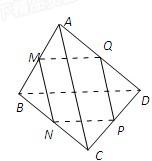 如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.