题目内容
某校一课题小组对西安市工薪阶层对“楼市限购令”态度进行调查,抽调了50人,他们月收入频数分布及对“楼市限购令”赞成人数如下表.
(1)完成下图的月收入频率分布直方图(注意填写纵坐标);
(2)若从收入(单位:百元)在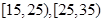 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为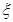 ,求随机变量
,求随机变量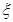 的分布列和数学期望.
的分布列和数学期望.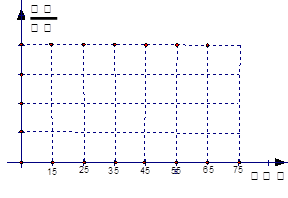
| 月收入 (单位:百元) | 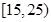 | 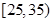 | 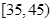 | 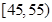 | 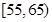 | 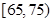 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 3 | 1 |
(2)若从收入(单位:百元)在
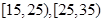 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为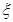 ,求随机变量
,求随机变量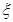 的分布列和数学期望.
的分布列和数学期望.
解:(1)各组的频率分别是 , ………………………2分
, ………………………2分
所以图中各组的纵坐标分别是: ,………………………3分
,………………………3分

………………………5分
(2)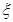 所有可能取值有0,1,2,3, ……………………6分
所有可能取值有0,1,2,3, ……………………6分
 , ……………………7分
, ……………………7分
 ……………………8分
……………………8分
 ……………………9分
……………………9分
 ……………………10分
……………………10分
所以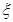 的分布列是
的分布列是
……………………11分
所以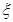 的期望值是
的期望值是 . ……………………12分
. ……………………12分
 , ………………………2分
, ………………………2分所以图中各组的纵坐标分别是:
 ,………………………3分
,………………………3分
………………………5分
(2)
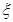 所有可能取值有0,1,2,3, ……………………6分
所有可能取值有0,1,2,3, ……………………6分 , ……………………7分
, ……………………7分 ……………………8分
……………………8分 ……………………9分
……………………9分 ……………………10分
……………………10分所以
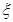 的分布列是
的分布列是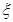 | 0 | 1 | 2 | 3 |
 |  |  |  |  |
所以
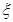 的期望值是
的期望值是 . ……………………12分
. ……………………12分本试题主要是考查了直方图的运用,以及分布列的求解和数学期望值的综合运用。
(1)直方图中面积代表频率,可知各组的频率分别是 ,然后得到各个组的纵坐标的值。
,然后得到各个组的纵坐标的值。
(2)先分析随机变量的可能取值,然后利用古典概型概率公式得到分布列和数学期望值。
(1)直方图中面积代表频率,可知各组的频率分别是
 ,然后得到各个组的纵坐标的值。
,然后得到各个组的纵坐标的值。(2)先分析随机变量的可能取值,然后利用古典概型概率公式得到分布列和数学期望值。

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目






 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)
 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.









 的值;
的值;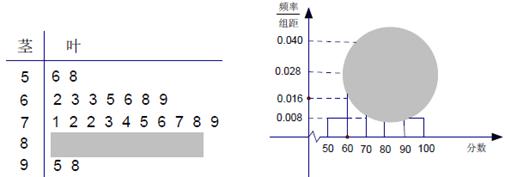
 之间的频数;
之间的频数;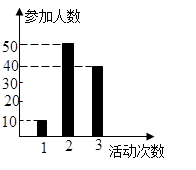
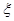 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量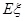 。
。 和
和 ,则新的一组数据2x1-3y1+1,2x2-3y2+1,…,2xn-3yn+1的平均数是( )
,则新的一组数据2x1-3y1+1,2x2-3y2+1,…,2xn-3yn+1的平均数是( )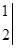
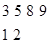 ,则该组数据的中位数为 .
,则该组数据的中位数为 .