题目内容
(本小题满分13分)
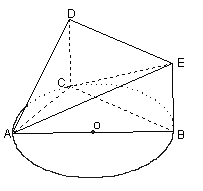
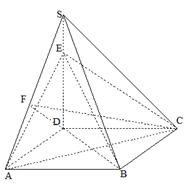 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
SD=2,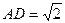 ,E是SD上的点.(Ⅰ)求证:AC⊥BE;
,E是SD上的点.(Ⅰ)求证:AC⊥BE;
(Ⅱ)求二面角C—AS—D的余弦值.
 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,
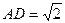 ,E是SD上的点.(Ⅰ)求证:AC⊥BE;
,E是SD上的点.(Ⅰ)求证:AC⊥BE;(Ⅱ)求二面角C—AS—D的余弦值.
(Ⅰ)见解析 (Ⅱ) 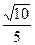
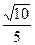
(Ⅰ)连结BD.因为底面ABCD是正方形,所以AC⊥BD.
因为SD⊥平面ABCD,AC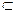 平面ABCD,
平面ABCD,
所以AC⊥SD.……2分又因为SD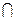 BD=D,
BD=D,
所以AC⊥平面BDS. 4分因为BE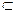 平面BDS,所以
平面BDS,所以 ⊥
⊥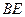 .……6分
.……6分
(Ⅱ)因为SD⊥平面ABCD,所以SD⊥CD.因为底面ABCD是正方形,
所以AD⊥CD.又因为SD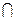 AD=D,所以CD⊥平面SAD,所以CD⊥AS.…8分过点D在平面SAD内作DF⊥AS于F,连结CF.由于,DF
AD=D,所以CD⊥平面SAD,所以CD⊥AS.…8分过点D在平面SAD内作DF⊥AS于F,连结CF.由于,DF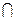 CD=D,所以AS⊥平面DCF。所以AS⊥CF.故∠CFD是二面角C—AS—D的平面角. 10分在Rt△ADS中,
CD=D,所以AS⊥平面DCF。所以AS⊥CF.故∠CFD是二面角C—AS—D的平面角. 10分在Rt△ADS中,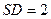 ,
,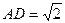 ,可求得
,可求得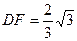 .
.
在Rt△CFD中,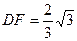 ,
,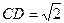 ,可求得
,可求得 .
.
所以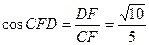 .即二面角C—AS—D的余弦值为
.即二面角C—AS—D的余弦值为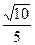 .… 12分
.… 12分
因为SD⊥平面ABCD,AC
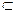 平面ABCD,
平面ABCD,所以AC⊥SD.……2分又因为SD
 BD=D,
BD=D,所以AC⊥平面BDS. 4分因为BE
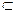 平面BDS,所以
平面BDS,所以 ⊥
⊥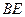 .……6分
.……6分(Ⅱ)因为SD⊥平面ABCD,所以SD⊥CD.因为底面ABCD是正方形,
所以AD⊥CD.又因为SD
 AD=D,所以CD⊥平面SAD,所以CD⊥AS.…8分过点D在平面SAD内作DF⊥AS于F,连结CF.由于,DF
AD=D,所以CD⊥平面SAD,所以CD⊥AS.…8分过点D在平面SAD内作DF⊥AS于F,连结CF.由于,DF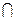 CD=D,所以AS⊥平面DCF。所以AS⊥CF.故∠CFD是二面角C—AS—D的平面角. 10分在Rt△ADS中,
CD=D,所以AS⊥平面DCF。所以AS⊥CF.故∠CFD是二面角C—AS—D的平面角. 10分在Rt△ADS中,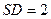 ,
,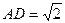 ,可求得
,可求得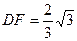 .
.在Rt△CFD中,
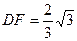 ,
,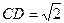 ,可求得
,可求得 .
.所以
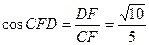 .即二面角C—AS—D的余弦值为
.即二面角C—AS—D的余弦值为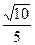 .… 12分
.… 12分
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
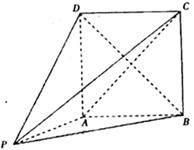
 中,四边形
中,四边形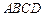 为矩形,
为矩形, 平面
平面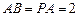 。
。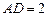 时,求证:平面
时,求证:平面 平面
平面 ;
; 与
与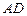 所成角为45°,求几何体
所成角为45°,求几何体
 平面ABC ,
平面ABC ,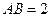 ,
,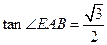 .
.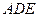 ;
;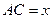 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求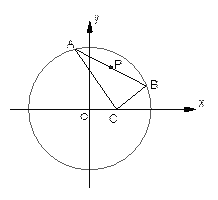
 (3)当
(3)当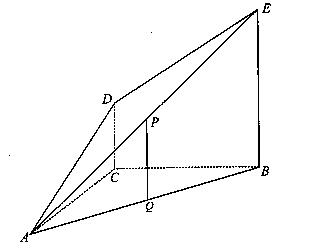
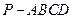 中,底面为菱形,
中,底面为菱形,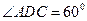 ,
,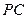 与底面
与底面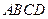 垂直,
垂直,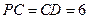 ,
,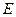 为棱
为棱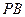 的中点,
的中点,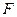 为
为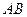 的中点,
的中点, 为
为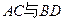 的交点,
的交点,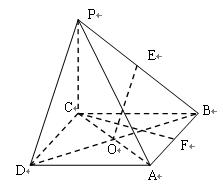
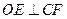 ;
;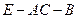 的余弦值.
的余弦值.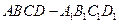 的棱长为3,点
的棱长为3,点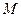 在
在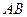 上,且
上,且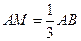 ,点
,点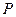 在平面
在平面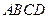 上,且动点
上,且动点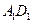 的距离与
的距离与 中,动点
中,动点
 体的三视图(单位:cm)如图所示,则此
体的三视图(单位:cm)如图所示,则此