题目内容
设a为实数,函数f(x)=x2+|x-a|+1 x∈R,(Ⅰ)讨论f(x)的奇偶性;
(Ⅱ)求f(x)的最小值.
解析:(Ⅰ)当a=0时,f(-x)=x2+|x|+1=f(x),此时f(x)为偶函数;当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a),且f(-a)≠-f(a),此时函数f(x)无奇偶性.
(Ⅱ)f(x)=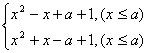
当x≤a时,f(x)=(x-![]() )2+a+
)2+a+![]() .
.
若a≤![]() ,f(x)在(-∞,a]上单调递减从而f(x)在(-∞,a)上的最小值为f(a)=a2+1;
,f(x)在(-∞,a]上单调递减从而f(x)在(-∞,a)上的最小值为f(a)=a2+1;
若a>![]() ,f(x)min=f(
,f(x)min=f(![]() )=a+
)=a+![]() ,且f(
,且f(![]() )≤f(a).
)≤f(a).
当x≥a时,f(x)=(x+![]() )2-a+
)2-a+![]() ,
,
若a≤-![]() ,f(x)min=f(-
,f(x)min=f(-![]() )=-a+
)=-a+![]() ,且f(-
,且f(-![]() )≤f(a);
)≤f(a);
若a>-![]() ,f(x)min=f(a)=a2+1.
,f(x)min=f(a)=a2+1.
综上a≤-![]() 时,f(x)min=
时,f(x)min=![]() -a;
-a;
-![]() <a≤
<a≤![]() 时,f(x)min=a2+1;
时,f(x)min=a2+1;
a>![]() 时,f(x)min=a+
时,f(x)min=a+![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目