Question

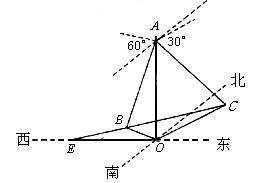
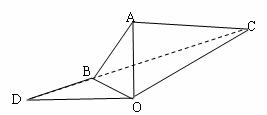
海岛O上有一座海拔1 km的小山，山顶设有一观察站A,上午11时测得一轮船在岛的北偏东60°的C处，俯角为30°；11时10分，又测得该船在岛的北偏西60°的B处，俯角为60°.

(1)求该船的速度；

(2)若此船以不变的船速继续前进，则它何时到达岛的正西方向？此时轮船所在点E离海岛O的距离是多少千米？

Answer 1

解：(1)如图在Rt△AOB和Rt△AOC中，OB=OAcot60°=,OC=OAcot30°=,在△BOC中，由余弦定理得

BC=.

∵由C到B用的时间为=(h),

∴该船的速度为= km/h.

(2)在△OBC中，由余弦定理，得

cos∠OBC==,

∴sin∠OBC==.

∴sin∠OEB=sin(∠OBE+∠EOB)=sin∠OBE·cos∠EOB+cos∠OBE·sin∠EOB=.

    在△BEO中，由正弦定理得

OE==，

BE=,

∴从B到E所需时间为：

÷=(h)=5(min).

答：船速为 km/h,该船于11时15分到达岛的正西方向，此时E离海岛O的距离是1.5 km.