题目内容
求当函数y=sin2x+acosx-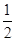 a-
a- 的最大值为1时a的值.
的最大值为1时a的值.
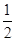 a-
a- 的最大值为1时a的值.
的最大值为1时a的值.y=1-cos2x+acosx-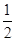 a-
a-
=-cos2x+acosx- -
-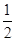
=-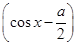 2+
2+ -
- -
-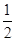 .
.
设cosx=t,∵-1≤cosx≤1,
∴-1≤t≤1.
∴y=-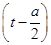 2+
2+ -
- -
-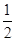 ,-1≤t≤1.………2分
,-1≤t≤1.………2分
(1)当 <-1,即a<-2时,t=-1,y有最大值-
<-1,即a<-2时,t=-1,y有最大值- a-
a- .
.
由已知条件可得- a-
a- =1,∴a=-
=1,∴a=-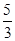 >-2(舍去). ……5分
>-2(舍去). ……5分
(2)当-1≤ ≤1时,即-2≤a≤2时,t=
≤1时,即-2≤a≤2时,t= ,y有最大值
,y有最大值 -
- -
-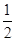 .
.
由已知条件可得 -
- -
-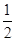 =1,解得a=1-
=1,解得a=1-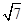 或a=1+
或a=1+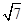 (舍去).……8分
(舍去).……8分
(3)当 >1,即a>2时,t=1,y有最大值
>1,即a>2时,t=1,y有最大值 -
- .
.
由已知条件可得 -
- =1,∴a=5. ………11分
=1,∴a=5. ………11分
综上可得a=1-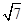 或a=5.
或a=5.
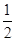 a-
a-
=-cos2x+acosx-
 -
-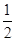
=-
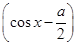 2+
2+ -
- -
-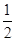 .
.设cosx=t,∵-1≤cosx≤1,
∴-1≤t≤1.
∴y=-
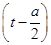 2+
2+ -
- -
-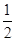 ,-1≤t≤1.………2分
,-1≤t≤1.………2分(1)当
 <-1,即a<-2时,t=-1,y有最大值-
<-1,即a<-2时,t=-1,y有最大值- a-
a- .
.由已知条件可得-
 a-
a- =1,∴a=-
=1,∴a=-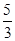 >-2(舍去). ……5分
>-2(舍去). ……5分(2)当-1≤
 ≤1时,即-2≤a≤2时,t=
≤1时,即-2≤a≤2时,t= ,y有最大值
,y有最大值 -
- -
-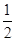 .
.由已知条件可得
 -
- -
-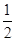 =1,解得a=1-
=1,解得a=1-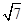 或a=1+
或a=1+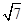 (舍去).……8分
(舍去).……8分(3)当
 >1,即a>2时,t=1,y有最大值
>1,即a>2时,t=1,y有最大值 -
- .
.由已知条件可得
 -
- =1,∴a=5. ………11分
=1,∴a=5. ………11分综上可得a=1-
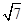 或a=5.
或a=5. 略

练习册系列答案
相关题目
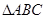 中,
中,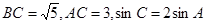
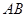 的值; (2)求
的值; (2)求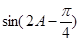 的值; (3)求
的值; (3)求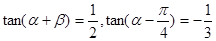 ,则
,则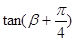 的值为 ( )
的值为 ( )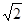
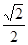
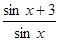 (0<x<π),求函数f(x)的值域;
(0<x<π),求函数f(x)的值域;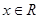 ,不等式
,不等式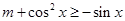 恒成立,求
恒成立,求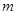 的取值范围。
的取值范围。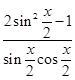 ,则f(
,则f(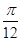 )的值为
)的值为 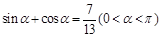 ,则
,则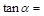 ( )
( )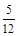
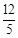
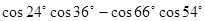 ;
;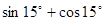 。
。 ,则
,则 的值是 .
的值是 . 等于 ( )
等于 ( )