题目内容
设a＞0，b＞0，则以下不等式中不恒成立的是
- A.
≥4 - B.a3+b3≥2ab2
- C.a2+b2+2≥2a+2b
- D.
≥
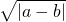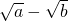
B
分析：根据基本不等式的性质可知．≥
排除A，取
，判断出B不成立．a2+b2+2-（2a+2b）=（a-1）2+（b-1）2≥排除C；看a＜b和a≥b，时D项均成立排除D．
解答：∵a＞0，b＞0，
∴A．≥≥4故A恒成立，
B．a3+b3≥2ab2，取，则B不成立
C．a2+b2+2-（2a+2b）=（a-1）2+（b-1）2≥0故C恒成立
D．若a＜b则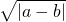≥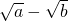恒成立
若a≥b，则
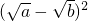=2
≥0，
∴≥
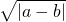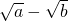
故D恒成立
点评：本题主要考查了基本不等式问题．考查了学生对基础知识的掌握．
分析：根据基本不等式的性质可知．
≥排除A，取，判断出B不成立．a2+b2+2-（2a+2b）=（a-1）2+（b-1）2≥排除C；看a＜b和a≥b，时D项均成立排除D．解答：∵a＞0，b＞0，
∴A．
≥≥4故A恒成立，B．a3+b3≥2ab2，取
，则B不成立C．a2+b2+2-（2a+2b）=（a-1）2+（b-1）2≥0故C恒成立
D．若a＜b则
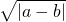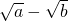≥恒成立若a≥b，则
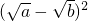=2≥0，∴
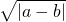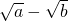
≥故D恒成立
点评：本题主要考查了基本不等式问题．考查了学生对基础知识的掌握．
练习册系列答案
相关题目
设a＞0，b＞0，则以下不等式中不恒成立的是（ ）
A、(a+b)(
| ||||||
| B、a3+b3≥2ab2 | ||||||
| C、a2+b2+2≥2a+2b | ||||||
D、
|
设a＞0，b＞0，则以下不等式中不一定成立的是（ ）
A、
| ||||
| B、ln（ab+1）＞0 | ||||
| C、a2+b2+2≥2a+2b | ||||
| D、a3+b3≥2ab2 |
设a＞0，b＞0，则下面不等式中不恒成立的是（ ）
A、
| ||||||||
| B、a2+b2+1＞a+b | ||||||||
C、
| ||||||||
D、
|