题目内容
过双曲线C:x2-
=1(b>0)的左顶点P作斜率为1的直线l,若l与双曲线C的两条渐近线分别相交于点Q,R,且
+
=2
,则双曲线C的离心率是( )
| y2 |
| b2 |
| OP |
| OR |
| OQ |
分析:先由双曲线线方程可得P的坐标和直线l的方程与双曲线的渐近线联立求得Q和R的横坐标,进而根据且
+
=2
,求得b的值,进而根据c=
求得c,最后根据离心率公式答案可得.
| OP |
| OR |
| OQ |
| a2+b2 |
解答:解:由题可知P(-1,0)所以直线L的方程为y=x+1,
两条渐近线方程为y=-bx或y=bx
联立y=x+1和y=-bx得Q的横坐标为xQ=-
同理得R的横坐标为xR=
,
∵
+
=2
,
∴(-1,0)+(
,yR)=2(-
,yQ),
∴-1+
=-
⇒b=3,c=
=
,
∴e=
=
,
故选B.
两条渐近线方程为y=-bx或y=bx
联立y=x+1和y=-bx得Q的横坐标为xQ=-
| 1 |
| b+1 |
同理得R的横坐标为xR=
| 1 |
| b-1 |
∵
| OP |
| OR |
| OQ |
∴(-1,0)+(
| 1 |
| b-1 |
| 1 |
| b+1 |
∴-1+
| 1 |
| b-1 |
| 2 |
| b+1 |
| 1+9 |
| 10 |
∴e=
| c |
| a |
| 10 |
故选B.
点评:本题主要考查了双曲线的简单性质.考查了学生综合分析问题的能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形;
的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;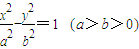 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.