题目内容
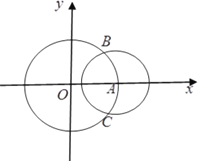
【题目】如图,在平面直角坐标系![]() 中,圆
中,圆![]() :
:![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,以点
,以点![]() 为圆心的圆
为圆心的圆![]() :
:![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 变化时,求
变化时,求![]() 的最小值;
的最小值;
(3)过点![]() 的直线
的直线![]() 与圆A切于点
与圆A切于点![]() ,与圆
,与圆![]() 分别交于点
分别交于点![]() ,
,![]() ,若点
,若点![]() 是
是![]() 的中点,试求直线
的中点,试求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】分析:(1)根据半径,得到圆A的标准方程;因为B、C是两个圆的交点,联立两个圆可得到两个交点坐标,利用两点间距离公式即可求得BC的长。
(2)根据圆A关于x轴对称,可设![]() ,代入到圆O中,用
,代入到圆O中,用![]() 表示
表示![]() ;根据向量数量积的坐标运算,得到
;根据向量数量积的坐标运算,得到![]() ,根据
,根据![]() 的取值范围即可得到
的取值范围即可得到![]() 的最小值。
的最小值。
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() ,可知
,可知![]() 与
与![]() 相似,根据中点性质和勾股定理,在
相似,根据中点性质和勾股定理,在![]() 和
和![]() 中,联立方程求得r的值;设出直线方程,根据点到直线距离公式即可求出直线方程。
中,联立方程求得r的值;设出直线方程,根据点到直线距离公式即可求出直线方程。
详解:(1)当![]() 时,
时,
由![]() 得,
得,![]()
![]()
![]()
(2)由对称性,设![]() ,则
,则![]()
所以![]()
![]()
![]()
因为![]() ,所以当
,所以当![]() 时,
时,![]() 的最小值为
的最小值为![]()
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]()
则![]() ,从而
,从而![]() ,不妨记
,不妨记![]() ,
,![]()
在![]() 中
中![]() 即
即![]() ①
①
在![]() 中
中![]() 即
即![]() ②
②
由①②解得![]()
由题直线![]() 的斜率不为0,可设直线
的斜率不为0,可设直线![]() 的方程为:
的方程为:![]() ,由点A到直线
,由点A到直线![]() 的距离等于
的距离等于![]()
则![]() ,所以
,所以![]() ,从而直线
,从而直线![]() 的方程为
的方程为![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目


