题目内容
【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若关于![]() 的不等式
的不等式![]() 只有两个整数解,求实数
只有两个整数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,最小值为
时,最小值为![]() ;当
;当![]() ,最小值为
,最小值为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)运用导数与单调性关系的有关知识求解;(2)借助题设条件运用分类整合的数学思想分析求解即可获解.
试题解析:
(1)![]() ,令
,令![]() 得
得![]() 的递增区间为
的递增区间为![]() ;
;
令![]() 得
得![]() 的递减区间为
的递减区间为![]() ,.2分 ∵
,.2分 ∵![]() ,则
,则
当![]() 时,
时, ![]() 在
在![]() 上为增函数,
上为增函数, ![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,又
上为减函数,又![]() ,
,
∴若![]() ,
, ![]() 的最小值为
的最小值为![]() ,...4分若
,...4分若![]() ,
, ![]() 的最小值为
的最小值为![]() ,
,
综上,当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ;当
;当![]() ,
, ![]() 的最小值为
的最小值为![]()
(2)由(1)知, ![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() ,
,
且在![]() 上
上![]() ,又
,又![]() ,则
,则![]() .又
.又![]() .
.
∴![]() 时,由不等式
时,由不等式![]() 得
得![]() 或
或![]() ,而
,而![]() 解集为
解集为![]() ,整数解有无数多个,不合题意;
,整数解有无数多个,不合题意;
![]() 时,由不等式
时,由不等式![]() 得
得![]() ,解集为
,解集为![]() ,
,
整数解有无数多个,不合题意;
![]() 时,由不等式
时,由不等式![]() 得
得![]() 或
或![]() ,
,
∵![]() 解集为
解集为![]() 无整数解,
无整数解,
若不等式![]() 有两整数解,则
有两整数解,则![]() ,
,
∴![]()
综上,实数![]() 的取值范围是
的取值范围是![]()

【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
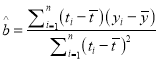 ,
, ![]()
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第x周)和市场占有率(y﹪)的几组相关数据如下表:
| 1 | 2 | 3 | 4 | 5 |
| 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
(Ⅰ)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测在第几周,该款旗舰机型市场占有率将首次超过 0.40﹪(最后结果精确到整数).
参考公式: ,
,![]()