题目内容
α,β为平面,m为直线,如果α∥β,那么“m∥α”是“m β”的
β”的
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件. |
B
解析试题分析:因为已知中α∥β,说明两个平面平行,那么又因为m∥α,则直线m可能在β内,也可能不在β内,因此说,条件不能推出结论,但是如果m β,则可知平行平面中的任何一条直线,都平行与另一个平面,故结论可以推出条件,因此可知选B。
β,则可知平行平面中的任何一条直线,都平行与另一个平面,故结论可以推出条件,因此可知选B。
考点:本试题主要是考查了面面平行的性质定理运用。
点评:一般来说给定面面平行,主要推导线面平行,以及线线平行的这样一个方向。同时根据需要,合理的进行证明。属于基础题。

练习册系列答案
相关题目
“a和b都不是奇数”的否定是( )
| A.a和b至少有一个奇数 | B.a和b至多有一个是奇数 |
| C.a是奇数,b不是奇数 | D.a和b都是奇数 |
已知P:|2x-3|<1, Q:x(x-3)<0, 则P是Q的( )
| A.充分不必要条件; | B.必要不充分条件 ; |
| C.充要条件 ; | D.既不充分也不必要条件 |
命题“若α= ,则tanα=1”的逆否命题是( )
,则tanα=1”的逆否命题是( )
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
若命题p: ,则┑p 为( )
,则┑p 为( )
A. | B. |
C. | D. |
已知命题p: ,则命题p的否定是( )
,则命题p的否定是( )
A.不存在 | B. |
C. | D. |
命题:“若 ,则
,则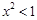 ”的逆否命题是( )
”的逆否命题是( )
A.若 则 则 | B.若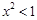 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
设命题 是
是 的充要条件;命题
的充要条件;命题 ,则( )
,则( )
A. 为真 为真 | B. 为真 为真 | C. 真 真 假 假 | D. 均为假 均为假 |


