题目内容
若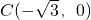 、
、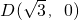 ,M是椭圆
,M是椭圆 上的动点,则
上的动点,则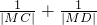 的最小值为________.
的最小值为________.
1
分析:由题设条件知椭圆 的焦点即为C,D两点,根据椭圆的定义得出|MC|+|MD|为定值,从而利用基本不等式得到
的焦点即为C,D两点,根据椭圆的定义得出|MC|+|MD|为定值,从而利用基本不等式得到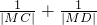 的最小值.
的最小值.
解答:由题设条件知焦点在x轴上,
故椭圆方程椭圆
由c= =
= ,
,
易知C,D两点是椭圆 的焦点,
的焦点,
所以,|MC|+|MD|=2a=4,
从而|MC|•|MD|≤( )2=22=4,
)2=22=4,
当且仅当|MC|=|MD|取等号,
即点M的坐标为(0,±1)时上式取等号,
∴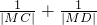 =
= ≥
≥ ,
,
则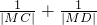 的最小值为 1.
的最小值为 1.
故答案为:1.
点评:本题考查圆锥曲线的综合应用,基本不等式及两点间的距离公式.解题时要认真审题,仔细求解.
分析:由题设条件知椭圆
 的焦点即为C,D两点,根据椭圆的定义得出|MC|+|MD|为定值,从而利用基本不等式得到
的焦点即为C,D两点,根据椭圆的定义得出|MC|+|MD|为定值,从而利用基本不等式得到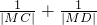 的最小值.
的最小值.解答:由题设条件知焦点在x轴上,
故椭圆方程椭圆

由c=
 =
= ,
,易知C,D两点是椭圆
 的焦点,
的焦点,所以,|MC|+|MD|=2a=4,
从而|MC|•|MD|≤(
 )2=22=4,
)2=22=4,当且仅当|MC|=|MD|取等号,
即点M的坐标为(0,±1)时上式取等号,
∴
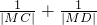 =
= ≥
≥ ,
,则
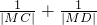 的最小值为 1.
的最小值为 1.故答案为:1.
点评:本题考查圆锥曲线的综合应用,基本不等式及两点间的距离公式.解题时要认真审题,仔细求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知以原点O为中心的椭圆的一条准线方程为
已知以原点O为中心的椭圆的一条准线方程为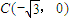 、
、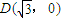 ,M是椭圆
,M是椭圆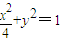 上的动点,则
上的动点,则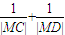 的最小值为 .
的最小值为 . ,离心率
,离心率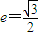 ,M是椭圆上的动点
,M是椭圆上的动点 ,求|MC|•|MD|的最大值;
,求|MC|•|MD|的最大值;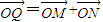 ,
, 、求线段QB的中点P的轨迹方程.
、求线段QB的中点P的轨迹方程.