题目内容
已知数列{an}的首项 ,
, .
.
(1)求证:数列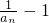 为等比数列;
为等比数列;
(2)记 ,若Sn<100,求最大的正整数n.
,若Sn<100,求最大的正整数n.
(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列且am-1,as-1,an-1成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
解:(1)∵ ,∴
,∴ ,(2分)
,(2分)
∵ ,∴
,∴ ,(3分)
,(3分)
∴ ,
,
∴数列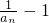 为等比数列.(4分)
为等比数列.(4分)
(2)由(1)可求得 ,∴
,∴ .(5分)
.(5分) =
= ,(7分)
,(7分)
若Sn<100,则 ,∴nmax=99.(9分)
,∴nmax=99.(9分)
(3)假设存在,则m+n=2s,(am-1)•(an-1)=(as-1)2,(10分)
∵ ,∴
,∴ .(12分)
.(12分)
化简得:3m+3n=2•3s,(13分)
∵ ,当且仅当m=n时等号成立.(15分)
,当且仅当m=n时等号成立.(15分)
又m,n,s互不相等,∴不存在.(16分)
分析:(1)根据an+1和an关系式进行化简,
(2)先由(1)得出数列{ }的通项公式,然后根据分组方法求出Sn,解不等式Sn<100即可;
}的通项公式,然后根据分组方法求出Sn,解不等式Sn<100即可;
(3)假设存在正整数m,s,n,根据等比数列性质得出(am-1)•(an-1)=(as-1)2并化简,再根据a+b≥2 ,确定是否存在.
,确定是否存在.
点评:本题考查了等比数列的性质、前n项和的求法以及不等式的解法,综合性很强,本题要注意a+b≥2 运用,本题有一定难度.
运用,本题有一定难度.
 ,∴
,∴ ,(2分)
,(2分)∵
 ,∴
,∴ ,(3分)
,(3分)∴
 ,
,∴数列
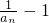 为等比数列.(4分)
为等比数列.(4分)(2)由(1)可求得
 ,∴
,∴ .(5分)
.(5分) =
= ,(7分)
,(7分)若Sn<100,则
 ,∴nmax=99.(9分)
,∴nmax=99.(9分)(3)假设存在,则m+n=2s,(am-1)•(an-1)=(as-1)2,(10分)
∵
 ,∴
,∴ .(12分)
.(12分)化简得:3m+3n=2•3s,(13分)
∵
 ,当且仅当m=n时等号成立.(15分)
,当且仅当m=n时等号成立.(15分)又m,n,s互不相等,∴不存在.(16分)
分析:(1)根据an+1和an关系式进行化简,
(2)先由(1)得出数列{
 }的通项公式,然后根据分组方法求出Sn,解不等式Sn<100即可;
}的通项公式,然后根据分组方法求出Sn,解不等式Sn<100即可;(3)假设存在正整数m,s,n,根据等比数列性质得出(am-1)•(an-1)=(as-1)2并化简,再根据a+b≥2
 ,确定是否存在.
,确定是否存在.点评:本题考查了等比数列的性质、前n项和的求法以及不等式的解法,综合性很强,本题要注意a+b≥2
 运用,本题有一定难度.
运用,本题有一定难度. 
练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目