题目内容
若关于x的一元二次方程x2-(m+1)x-m=0有两个不相等的实数根,则m的取值范围是
(-∞,-3-2
)∪(-3+2
,+∞)
| 2 |
| 2 |
(-∞,-3-2
)∪(-3+2
,+∞)
.| 2 |
| 2 |
分析:利用判别式大于0,解不等式,即可求得m的取值范围.
解答:解:∵关于x的一元二次方程x2-(m+1)x-m=0有两个不相等的实数根,
∴△=(m+1)2+4m>0
∴m2+6m+1>0
∴m<-3-2
或m>-3+2
故答案为:(-∞,-3-2
)∪(-3+2
,+∞).
∴△=(m+1)2+4m>0
∴m2+6m+1>0
∴m<-3-2
| 2 |
| 2 |
故答案为:(-∞,-3-2
| 2 |
| 2 |
点评:本题考查一元二次方程根的情况,考查解不等式,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 的单调区间.
的单调区间.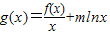 的单调区间.
的单调区间. -2(a-2)x-b
-2(a-2)x-b +16=0.
+16=0.