题目内容
(09年朝阳区二模文)(13分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)设![]() ,若对于任意
,若对于任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解析:(Ⅰ)因为![]()
所以![]() .
.
令![]() 解得
解得![]() .
.
因为当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,
,![]() 的单调减区间是
的单调减区间是![]() .
.
所以![]() 是
是![]() 的极大值,
的极大值,![]() 是
是![]() 的极小值. …………7分
的极小值. …………7分
(Ⅱ)![]() .
.
由已知![]()
![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
即 ![]() 恒成立.
恒成立.
因为![]() ,所以
,所以![]() ,(当且仅当
,(当且仅当![]() 时取“=”号),
时取“=”号),
所以![]() 的最小值为2. 由
的最小值为2. 由![]() ,得
,得![]() ,
,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

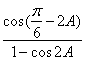 的值.
的值.