题目内容
已知菱形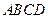 的顶点
的顶点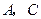 在椭圆
在椭圆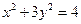 上,对角线
上,对角线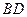 所在直线的斜率为1.
所在直线的斜率为1.
(Ⅰ)当直线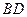 过点
过点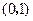 时,求直线
时,求直线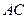 的方程;
的方程;
(Ⅱ)当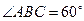 时,求菱形
时,求菱形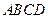 面积的最大值.
面积的最大值.
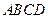 的顶点
的顶点 在椭圆
在椭圆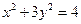 上,对角线
上,对角线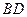 所在直线的斜率为1.
所在直线的斜率为1.(Ⅰ)当直线
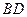 过点
过点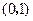 时,求直线
时,求直线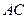 的方程;
的方程;(Ⅱ)当
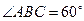 时,求菱形
时,求菱形 面积的最大值.
面积的最大值. (1)直线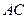 的方程:
的方程: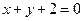 ;(2)
;(2)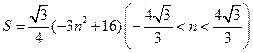 。
。
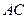 的方程:
的方程: ;(2)
;(2)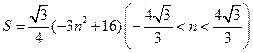 。
。Ⅰ)由题意得直线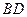 的方程为
的方程为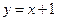 .
.
因为四边形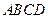 为菱形,所以
为菱形,所以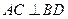 .
.
于是可设直线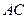 的方程为
的方程为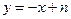 .
.
由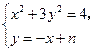 得
得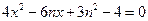 .
.
因为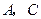 在椭圆上,
在椭圆上,
所以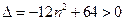 ,解得
,解得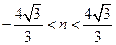 .
.
设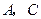 两点坐标分别为
两点坐标分别为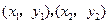 ,
,
则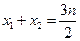 ,
,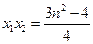 ,
,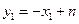 ,
,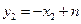 .
.
所以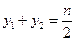 .
.
所以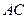 的中点坐标为
的中点坐标为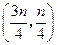 .
.
由四边形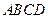 为菱形可知,点
为菱形可知,点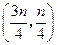 在直线
在直线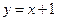 上,
上,
所以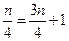 ,解得
,解得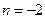 .
.
所以直线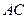 的方程为
的方程为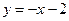 ,即
,即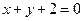 .
.
(Ⅱ)因为四边形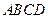 为菱形,且
为菱形,且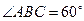 ,
,
所以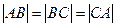 .
.
所以菱形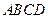 的面积
的面积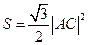 .
.
由(Ⅰ)可得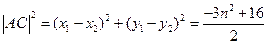 ,
,
所以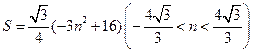
 的方程为
的方程为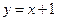 .
.因为四边形
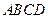 为菱形,所以
为菱形,所以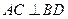 .
.于是可设直线
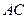 的方程为
的方程为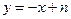 .
.由
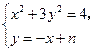 得
得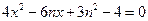 .
.因为
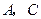 在椭圆上,
在椭圆上,所以
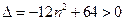 ,解得
,解得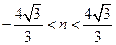 .
.设
 两点坐标分别为
两点坐标分别为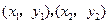 ,
,则
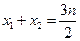 ,
,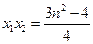 ,
,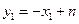 ,
,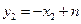 .
.所以
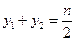 .
.所以
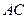 的中点坐标为
的中点坐标为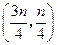 .
.由四边形
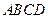 为菱形可知,点
为菱形可知,点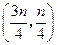 在直线
在直线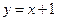 上,
上, 所以
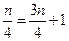 ,解得
,解得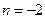 .
.所以直线
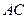 的方程为
的方程为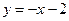 ,即
,即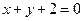 .
.(Ⅱ)因为四边形
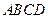 为菱形,且
为菱形,且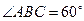 ,
,所以
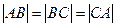 .
.所以菱形
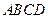 的面积
的面积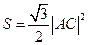 .
.由(Ⅰ)可得
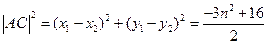 ,
,所以
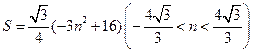

练习册系列答案
相关题目
 为菱形,
为菱形,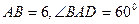 ,两个正三棱锥
,两个正三棱锥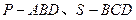 (底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点
(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点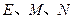 分别在
分别在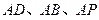 上,且
上,且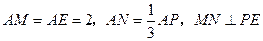 .
.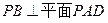 ;
;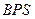 与底面
与底面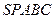 的体积.
的体积. 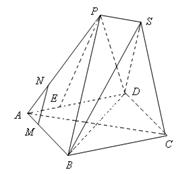
 中,
中,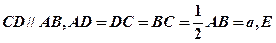 是
是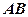 的中点,将
的中点,将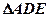 沿
沿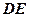 折起,使点
折起,使点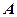 到点
到点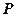 的位置,使二面角
的位置,使二面角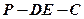 的大小为
的大小为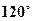
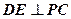 ;
;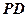 与平面
与平面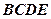 所成角的正弦值
所成角的正弦值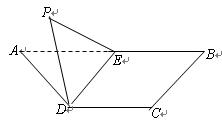
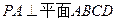 ,底面ABCD是直角梯形,
,底面ABCD是直角梯形, ,且AB∥CD,
,且AB∥CD,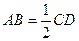 , 点F为线段PC的中点,
, 点F为线段PC的中点, 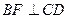 。
。 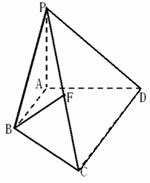
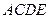 所在的平面与平面
所在的平面与平面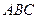 垂直,
垂直,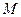 是
是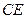 和
和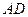 的交点,
的交点,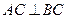 ,且
,且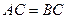 .
.
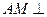 平面
平面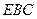 ; (2)求直线
; (2)求直线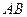 与平面
与平面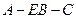 的大小.
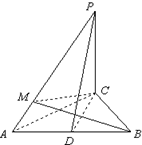
的大小.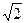 ,PB⊥PD.
,PB⊥PD.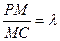 ,问
,问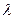 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.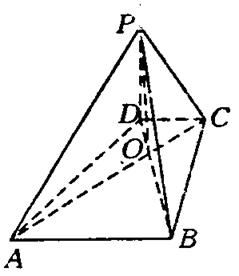
 中,
中, 底面
底面 ,
,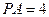 正方形的边长为2
正方形的边长为2 到平面
到平面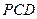 的距离;
的距离;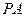 与平面
与平面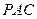 为半平面的二面角的正切值。
为半平面的二面角的正切值。
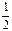 V的水。
V的水。