题目内容
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同。每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率;②获奖的概率。
(2)求在两次游戏中获奖次数X的分布列及数学期望E(x)。
(1) ① 设“在1次游戏中摸出i个白球”为事件![]() (i = 0 , 1, 2, 3), 则
(i = 0 , 1, 2, 3), 则
P(![]() ) =
) = ![]() ……………………3分
……………………3分
② 设“在1次游戏中获奖为事件B” 则B = ![]()
又P(![]() ) =
) = ![]() 且
且![]() ,
, ![]() 互斥,
互斥,
所以![]() ………………6分
………………6分
(2)由题意可知X的所有可能取值为0, 1,2
![]()
![]()
![]()
所以x 的分布列是
| x | 0 | 1 | 2 |
| P |
|
|
|
X的数学期望是E(X) = ![]() …………………………12分
…………………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
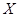 的分布列及数学期望
的分布列及数学期望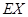 .
.