题目内容
函数f(x)=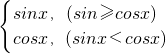 给出下列四个命题,其中正确的是
给出下列四个命题,其中正确的是
- A.f(x)的值域为[-1.1]
- B.f(x)是以π为周期的周期函数
- C.当且仅当x=2kx+
 (k∈Z)时,f(x)取得最大值
(k∈Z)时,f(x)取得最大值 - D.当且仅当2kx+π<x<2kx+
 ((k∈Z))时,f(x)<0
((k∈Z))时,f(x)<0
D
分析:由题意作出此分段函数的图象,由图象研究该函数的性质,依据这些性质判断四个命题的真假.此函数取自变量相同时函数值大的那一个,由此可顺利作出函数图象.
解答:由题意函数f(x)=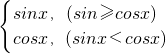 ,画出f(x)的图象,
,画出f(x)的图象,
图中实线部分.观察图象可知:
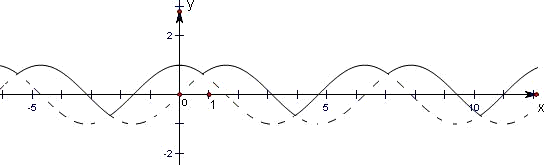
∵f(x+2π)=f(x),但是f(x+π)≠f(x),
∴函数f(x)的最小正周期为2π,故A错误;
由图象知,在x= +2kπ(k∈Z)时,函数图象位于最低点,
+2kπ(k∈Z)时,函数图象位于最低点,
该函数取得最小值sin( +2kπ)=-
+2kπ)=- ,
,
∴B错误;
由图象知,当且仅当x=2kx或x=2kx+ (k∈Z)时,函数图象位于最高点1,
(k∈Z)时,函数图象位于最高点1,
∴f(x)取得最大值1,
∴C错;
∵在2kx+π<x<2kx+ ((k∈Z))时,函数图象在x轴下方,
((k∈Z))时,函数图象在x轴下方,
∴f(x)<0,
∴D正确.
故选D.
点评:本题考点是三角函数的最值,本题是函数图象的运用,由函数的图象研究函数的性质,并以由图象研究出的结论判断和函数有关的命题的真假.
分析:由题意作出此分段函数的图象,由图象研究该函数的性质,依据这些性质判断四个命题的真假.此函数取自变量相同时函数值大的那一个,由此可顺利作出函数图象.
解答:由题意函数f(x)=
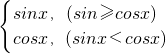 ,画出f(x)的图象,
,画出f(x)的图象,图中实线部分.观察图象可知:

∵f(x+2π)=f(x),但是f(x+π)≠f(x),
∴函数f(x)的最小正周期为2π,故A错误;
由图象知,在x=
 +2kπ(k∈Z)时,函数图象位于最低点,
+2kπ(k∈Z)时,函数图象位于最低点,该函数取得最小值sin(
 +2kπ)=-
+2kπ)=- ,
,∴B错误;
由图象知,当且仅当x=2kx或x=2kx+
 (k∈Z)时,函数图象位于最高点1,
(k∈Z)时,函数图象位于最高点1,∴f(x)取得最大值1,
∴C错;
∵在2kx+π<x<2kx+
 ((k∈Z))时,函数图象在x轴下方,
((k∈Z))时,函数图象在x轴下方,∴f(x)<0,
∴D正确.
故选D.
点评:本题考点是三角函数的最值,本题是函数图象的运用,由函数的图象研究函数的性质,并以由图象研究出的结论判断和函数有关的命题的真假.

练习册系列答案
相关题目