题目内容

已知数列{xn}满足x2=,xn=(xn-1+xn-2),n=3,4,….若xn=2,则x1等于(    )

A.                  B.3                  C.4                 D.5

剖析:由xn=(xn-1+xn-2)可找出相邻两项之间的递推关系,再进一步求xn,利用xn=2可求x1.

解析:xn=(xn-1+xn-2),两边减去xn-1得xn-xn-1=-(xn-1-xn-2),

    ∴=-,即{xn-xn-1}是以x2-x1为首项,公比为-的等比数列,

    xn-xn-1=(-)(-)n-2.

    x2-x1=-,

    x3-x2=-(-),

    ∴x4-x3=-(-)2,

    ……

    xn-xn-1=(-)(-)n-2.

    相加得xn-x1=-·=.                          (*)

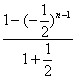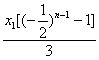    ∵xn=2,(*)式两边取极限,得2-x1=-,

    ∴x1=3.

答案:B

练习册系列答案
相关题目
10、已知数列{xn}满足xn+1=xn-xn-1（n≥2），x1=a，x2=b，Sn=x1+x2+…+xn，则下面正确的是（　　）
已知数列{xn}满足x2=
1
2
x1，xn=
1
2
（xn-1+xn-2）（n=3，4，5，…），若
lim
n→∞
xn=2，则x1=
 
．
数列{an}中，如果存在非零常数T，使得an+T=an对于任意的非零自然数n均成立，那么就称数列{an}为周期数列，其中T叫做数列{an}的周期．已知数列{xn}满足xn+1=|xn-xn-1|（n≥2），如果x1=1，x2=a（a∈R，a≠0），当数列{xn}的周期为3时，求该数列前2009项和是
1339+a
1339+a
．
已知数列{xn}满足：x1=1且xn+1=
xn+4
xn+1
，n∈N*．
（1）计算x2，x3，x4的值；
（2）试比较xn与2的大小关系；
（3）设an=|xn-2|，Sn为数列{an}前n项和，求证：当n≥2时，Sn≤2-
2
2n
．
已知数列{xn}满足：x1∈(0，1)，xn+1=
xn(
x
2
n
+3)
3
x
2
n
+1
(n∈N*）．
（1）证明：对任意的n∈N*，恒有xn∈（0，1）；
（2）对于n∈N*，判断xn与xn+1的大小关系，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网