题目内容
已知曲线C1:y=ax2+b和曲线C2:y=2blnx(a,b∈R)均与直线l:y=2x相切.(1)求实数a、b的值;
(2)设直线x=t(t>0)与曲线C1,C2及直线l分别相交于点M,N,P,记f(t)=|MP|-|NP|,求f(t)在区间(0,e](e为自然对数的底)上的最大值.
分析:(1)由题意及导数的几何含义可以先设出两个切点的坐标,利用条件建立a,b方程解出即可;
(2)由题意直线x=t(t>0)与曲线C1,C2及直线l分别相交于点M,N,P,可以联立直线方程与曲线方程及直线方程,求出M,N,P的坐标,利用两点间的距离公式得到
(t)=|MP|-|NP|的函数表达式,在有定义域求出值域即可.
(2)由题意直线x=t(t>0)与曲线C1,C2及直线l分别相交于点M,N,P,可以联立直线方程与曲线方程及直线方程,求出M,N,P的坐标,利用两点间的距离公式得到
(t)=|MP|-|NP|的函数表达式,在有定义域求出值域即可.
解答:解:(1)设曲线C1,C2与直线l相切的切点分别是(t1,at12+b),(t2,2blnt2),
则at12+b=2t1,at22+b=2t2
对函数分别求导可得,y'=2at,y′=
则
?
,
所以切线方程分别为:y-
=2(x-
),y-2blnb=2(x-b),即为y=2x
所以
∴
(2)由(1)可得线C1:y=
x2+e和曲线C2:y=2elnx,L;y=2x
由题意可以得到:
,
,
∴M(t,
+e),N(t,2elnt),P(t,2t),
所以f(t)=|MP|-|NP|=
t2-4t+2elnt+e,f′(t)=
-4+
≥0在t∈(0,e]恒成立
所以函数f(t)在定义域上位单调递增函数,所以(f(t)max=f(e)=0.
则at12+b=2t1,at22+b=2t2
对函数分别求导可得,y'=2at,y′=
| 2b |
| x |
则
|
|
所以切线方程分别为:y-
| 1 |
| a |
| 1 |
| a |
所以
|
∴
|
(2)由(1)可得线C1:y=
| 1 |
| e |
由题意可以得到:
|
|
|
∴M(t,
| t2 |
| e |
所以f(t)=|MP|-|NP|=
| 1 |
| e |
| 2t |
| e |
| 2e |
| t |
所以函数f(t)在定义域上位单调递增函数,所以(f(t)max=f(e)=0.
点评:此题考查了导数的几何含义及利用方程的思想求解未知的变量的知,还考查了联立方程解交点,及利用导函数求出函数的单调性并利用单调性求出函数的最大值.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.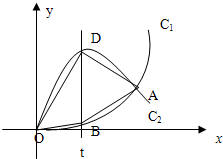 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=