题目内容
己知实数m是常数,(x-
)5的二项展开式中x3的系数等于10,则
=( )
| m |
| x |
| lim |
| x→0 |
| x2+x+3m |
| x+m |
| A、9 | B、7 | C、5 | D、3 |
分析:实数m是常数,(x-
)5的二项展开式中,x3的系数等于10能求出m=-2,
=
=
(x+3)=3.
| m |
| x |
| lim |
| x→0 |
| x2+x+3m |
| x+m |
| lim |
| x→0 |
| x2+x-6 |
| x-2 |
| lim |
| x→0 |
解答:解:Tr+1=
x5-r(-
)r=(-m)rC5rx5-2r,
5-2r=3,r=1,
(-m)1C54=0,m=0.
∴
=
=
(x+1)=1.
故答案为:1.
| C | r 5 |
| m |
| x |
5-2r=3,r=1,
(-m)1C54=0,m=0.
∴
| lim |
| x→0 |
| x2+x+3m |
| x+m |
=
| lim |
| x→0 |
| x2+x |
| x |
=
| lim |
| x→0 |
故答案为:1.
点评:本题考查二项式定理的性质和应用,解题时要注意极限的合理运用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
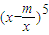 的二项展开式中,x3的系数等于10,则
的二项展开式中,x3的系数等于10,则 =( )
=( )