题目内容
若直线y=kx-1与双曲线x2-y2=4只有一个公共点，则k的取值范围为 ．
【答案】分析：由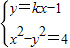
，得（1-k2）x2+2kx-5=0，则该方程只有一解，分1-k2=0，1-k2≠0两种情况讨论可解得k值．
解答：解：由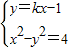
，得（1-k2）x2+2kx-5=0，
①当1-k2=0，即k=±1时，x=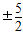
，
此时直线与双曲线相交，只有一个公共点；
②当1-k2≠0，即k≠±1时，
△=4k2-4（1-k2）（-5）=0，即4k2=5，解得k=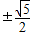
，
此时直线与双曲线相切，只有一个公共点；
综上，k的取值范围为{-1，1，-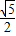
，
}．
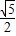故答案为：{-1，1，-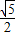
，
}．
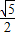点评：本题考查直线与圆锥曲线的位置关系，考查方程思想，考查函数解决问题的能力．
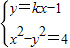，得（1-k2）x2+2kx-5=0，则该方程只有一解，分1-k2=0，1-k2≠0两种情况讨论可解得k值．解答：解：由
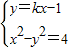，得（1-k2）x2+2kx-5=0，①当1-k2=0，即k=±1时，x=
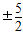，此时直线与双曲线相交，只有一个公共点；
②当1-k2≠0，即k≠±1时，
△=4k2-4（1-k2）（-5）=0，即4k2=5，解得k=
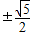，此时直线与双曲线相切，只有一个公共点；
综上，k的取值范围为{-1，1，-
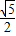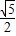，}．故答案为：{-1，1，-
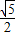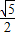，}．点评：本题考查直线与圆锥曲线的位置关系，考查方程思想，考查函数解决问题的能力．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
若直线y=kx+1与圆x2+y2=1相交于P、Q两点，且∠POQ=120°（其中O为原点），则k的值为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|