题目内容
(16分)已知函数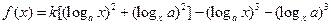 , (其中
, (其中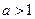 ),
),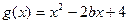 ,设
,设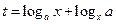 .
.
(Ⅰ)当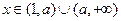 时,试将
时,试将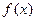 表示成
表示成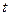 的函数
的函数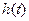 ,并探究函数
,并探究函数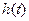 是否有极值;
是否有极值;
(Ⅱ)当k=4时,若对任意的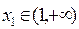 ,存在
,存在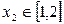 ,使
,使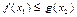 ,试求实数b的取值范围.。
,试求实数b的取值范围.。
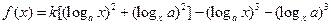 , (其中
, (其中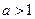 ),
),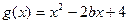 ,设
,设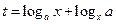 .
. (Ⅰ)当
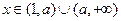 时,试将
时,试将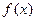 表示成
表示成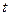 的函数
的函数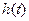 ,并探究函数
,并探究函数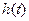 是否有极值;
是否有极值;(Ⅱ)当k=4时,若对任意的
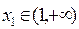 ,存在
,存在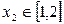 ,使
,使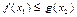 ,试求实数b的取值范围.。
,试求实数b的取值范围.。(Ⅰ)无极值
(Ⅱ)
(Ⅱ)

解:(Ⅰ)∵ ,
,
 ,
,
∴ ∴
∴
设 是
是 的两根,则
的两根,则 ,∴
,∴ 在定义域内至多有一解,
在定义域内至多有一解,
欲使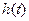 在定义域内有极值,只需
在定义域内有极值,只需 在
在 内有解,且
内有解,且 的值在根的左右两侧异号,∴
的值在根的左右两侧异号,∴ 得
得 综上:当
综上:当 时
时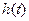 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当 时
时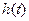 在定义域内无极值
在定义域内无极值
(Ⅱ)∵对任意的 ,存在
,存在 ,使
,使 等价于
等价于
 时,f(x)max
时,f(x)max
又k=4时,h(t)=-t3+4t2+3t-8 (t ,
,

∴h(t)max="h(3)=10,"

∴ ∴
∴
 ,
, ,
,∴
 ∴
∴
设
 是
是 的两根,则
的两根,则 ,∴
,∴ 在定义域内至多有一解,
在定义域内至多有一解,欲使
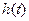 在定义域内有极值,只需
在定义域内有极值,只需 在
在 内有解,且
内有解,且 的值在根的左右两侧异号,∴
的值在根的左右两侧异号,∴ 得
得 综上:当
综上:当 时
时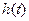 在定义域内有且仅有一个极值,当
在定义域内有且仅有一个极值,当 时
时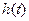 在定义域内无极值
在定义域内无极值(Ⅱ)∵对任意的
 ,存在
,存在 ,使
,使 等价于
等价于 时,f(x)max
时,f(x)max
又k=4时,h(t)=-t3+4t2+3t-8 (t
 ,
,

∴h(t)max="h(3)=10,"

∴
 ∴
∴

练习册系列答案
相关题目
 已知
已知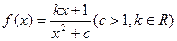 恰有一个极大值点和一个极小值点,其中的一个极值点是
恰有一个极大值点和一个极小值点,其中的一个极值点是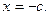
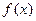 的另一个极值点;
的另一个极值点;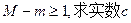 的取值范围.
的取值范围.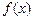 的定义域为
的定义域为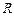 ,导函数
,导函数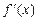 的图像如图所示,给出函数
的图像如图所示,给出函数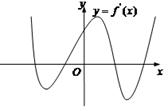
 函数
函数 在
在 处有极小值
处有极小值 ,则
,则 .
.
 的单调减区间;
的单调减区间;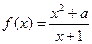 在
在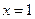 处取得极值,则实数
处取得极值,则实数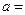 ▲ .
▲ . 在闭区间[-3,0]上的最大值、最小值分别是 、 。
在闭区间[-3,0]上的最大值、最小值分别是 、 。 在区间
在区间 上的最小值是 .
上的最小值是 .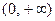 上的三个函数
上的三个函数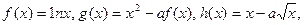 且
且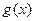 在
在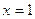 处取得极值.
处取得极值. 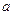 的值及函数
的值及函数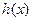 的单调区间;
的单调区间;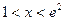 时,恒有
时,恒有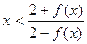 成立;
成立;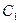 按向量
按向量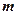
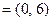 平移后得到曲线
平移后得到曲线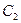 ,求
,求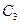 的交点个数,并说明理由.
的交点个数,并说明理由.