题目内容

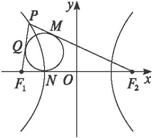
在双曲线C：-=1上任取一点P与其两个焦点F1、F2构成△PF1F2，△PF1F2的内切圆交F1F2于点N，求N的坐标.

思路解析：画图、观察，只需确定|ON|的长即可.利用双曲线定义及平面几何知识，有|PF2|-|PF1|=|NF2|-|NF1|.

解：如图所示，由圆的切线长定理,得

|PM|=|PQ|,|F1Q|=|F1N|,|F2M|=|F2N|.

∵P在双曲线上，

∴||PF1|-|PF2||

=|（|PQ|+|QF1|）-（|PM|+|MF2|）|

=||QF1|-|MF2||

=||NF1|-|NF2||.

∴N在双曲线上.

又点N在F1F2即x轴上.

∴点N是双曲线与x轴的交点.

令y=0代入双曲线方程得x=±4.

∴N（±4，0）.

方法归纳

    关于双曲线的问题，当条件中有双曲线上的点与焦点连线时，常联想到双曲线定义.

练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
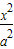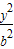b2
=1(a＞b＞0)的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似三角形，则称这两个椭圆为“相似椭圆”，且特征三角形的相似比即为相似椭圆的相似比．已知椭圆C1
x2
a2
+
y2
b2
=1以抛物线y2=4
3
x的焦点为一个焦点，且椭圆上任意一点到两焦点的距离之和为4．（1）若椭圆C2与椭圆C1相似，且相似比为2，求椭圆C2的方程．
（2）已知点P（m，n）（mn≠0）是椭圆C1上的任一点，若点Q是直线y=nx与抛物线x2=
1
mn
y异于原点的交点，证明点Q一定落在双曲线4x2-4y2=1上．
（3）已知直线l：y=x+1，与椭圆C1相似且短半轴长为b的椭圆为Cb，是否存在正方形ABCD，使得A，C在直线l上，B，D在曲线Cb上，若存在求出函数f（b）=SABCD的解析式及定义域，若不存在，请说明理由．
已知△ABC的顶点A（-5，0），B（5，0），顶点C在双曲线
x2
16
-
y2
9
=1上，则
sinA-sinB
sinC
=
±
8
5
±
8
5
．
如图，双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线为l1，l2，离心率为
13
3
，P1∈l1，P2∈l2，且
OP1
•
OP2
=t，
P2P
=λ
PP1
（λ＞0），P在双曲线C右支上．
（1）若△P1OP2的面积为6，求t的值；
（2）t=5时，求a最大时双曲线C的方程．
已知点（2，3）在双曲线C：-=1（a＞0，b＞0）上，C的焦距为4，则它的离心率为    ．
如图，双曲线C：（a＞0，b＞0）的渐近线为l1，l2，离心率为，P1∈l1，P2∈l2，且，（λ＞0），P在双曲线C右支上．
（1）若△P1OP2的面积为6，求t的值；
（2）t=5时，求a最大时双曲线C的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网