题目内容
16.已知实数x,y满足关系式xy-x-y=1,求x2+y2的最小值.分析 由xy-x-y=1可得xy=1+x+y,令x+y=t,则y=t-x,可得x2-tx+t+1=0,由△≥0可得t的范围,x2+y2=(t-1)2-3,由二次函数的知识可得.
解答 解:由xy-x-y=1可得xy=1+x+y,令x+y=t,则y=t-x,
代入上式可得x(t-x)=1+t,整理可得x2-tx+t+1=0,
由△=(-t)2-4(t+1)≥0可得t≥2+2$\sqrt{2}$或t≤2-2$\sqrt{2}$,
∴x2+y2=(x+y)2-2xy=(x+y)2-2(x+y)-2=t2-2t-2=(t-1)2-3
由二次函数的知识可知当t=2-2$\sqrt{2}$时,函数取最小值6-4$\sqrt{2}$
点评 本题考查距离公式,涉及换元法和一元二次方程根的存在性,属中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
6.用更相减损术得111与148的最大公约数为( )
| A. | 1 | B. | 17 | C. | 23 | D. | 37 |
6.在直棱柱(侧棱垂直于底面)ABC-A1B1C1中,点D为BC的中点,BC=4,AB=AC=$\sqrt{7}$,AA1=3,则三棱锥C1-AB1D的高为( )
| A. | $\sqrt{3}$ | B. | $\frac{6\sqrt{13}}{13}$ | C. | $\frac{12\sqrt{13}}{13}$ | D. | $\frac{\sqrt{39}}{13}$ |
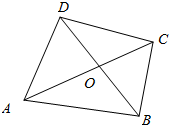 如图所示,在四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,对角线AC与BD交于点O,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
如图所示,在四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,对角线AC与BD交于点O,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.