题目内容
函数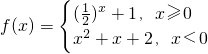
图象与函数g（x）=a的图象有三个不同的交点，则a的取值范围是________．
（
，2）
分析：由函数f（x）的解析式求出函数的值域，由题意可得，f（x）的图象和直线y=a有3个交点，数形结合求出a的取值范围．
解答：
解：由函数f（x）的解析式可得，当x≥0时，1＜f（x）≤2．当 x＜0时，f（x）=
≥．
由题意可得，f（x）的图象和直线y=a有3个交点，如图所示：
故有＜a＜2，
故答案为（，2）．
点评：本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．
，2）分析：由函数f（x）的解析式求出函数的值域，由题意可得，f（x）的图象和直线y=a有3个交点，数形结合求出a的取值范围．
解答：
解：由函数f（x）的解析式可得，当x≥0时，1＜f（x）≤2．当 x＜0时，f（x）=≥．由题意可得，f（x）的图象和直线y=a有3个交点，如图所示：
故有
＜a＜2，故答案为（
，2）．点评：本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
函数y=f（x）的图象与函数g（x）=log2x（x＞0）的图象关于原点对称，则f（x）的表达式为（ ）
A、f(x)=
| ||
B、f(x)=
| ||
| C、f（x）=-log2x（x＞0） | ||
| D、f（x）=-log2（-x）（x＜0） |
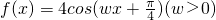图象与函数g（x）=2sin（2x+φ）+1的图象的对称轴完全相同．
时，求函数f（x）的值域．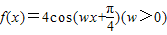
图象与函数g（x）=2sin（2x+φ）+1的图象的对称轴完全相同．
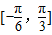时，求函数f（x）的值域．
的图象与函数g（x）=lg（-x）+2的图象关于直线l对称；