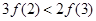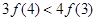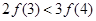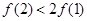题目内容
已知函数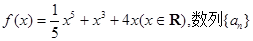 是等差数列,
是等差数列, 的值
的值
| A.恒为正数 | B.恒为负数 | C.恒为O | D.可正可负 |
A
解析试题分析:
 恒成立,函数
恒成立,函数 在R上是增函数,
在R上是增函数, 又函数
又函数 是奇函数,图像关于原点对称,结合图像可知
是奇函数,图像关于原点对称,结合图像可知 所以
所以 恒为正数
恒为正数
考点:函数性质及等差数列的考查
点评:本题的两个关键点:结合函数单调性奇偶性得到 ,结合函数图象等差数列性质得到
,结合函数图象等差数列性质得到

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知定义在R上的函数 满足
满足 ,如图表示该函数在区间
,如图表示该函数在区间 上的图象,则
上的图象,则 等于
等于
| A.3 | B.2 | C.1 | D.0 |
设函数 为定义在
为定义在 上的奇函数,对任意
上的奇函数,对任意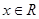 都有
都有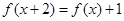 成立,则
成立,则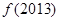 的值为( )
的值为( )
A.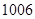 | B.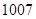 | C.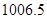 | D.无法确定 |
若2x-3-x≥2-y-3y,则
| A.x-y≥0 | B.x-y≤0 | C.x+y≥0 | D.x+y≤0 |
如图,矩形纸板ABCD的顶点A、B分别在正方形边框EOFG的边OE、OF上,当点B在OF边上进行左右运动时,点A随之在OE上进行上下运动.若AB=8,BC=3,运动过程中,则点D到点O距离的最大值为
A. | B.9 | C. | D. |
下列4对函数中表示同一函数的是( )
A.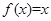 , , 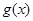 = =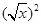 | B.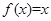 , ,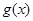  = = |
C. = =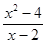 , ,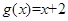 | D.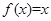 , , 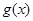 = =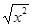 |
 上的函数
上的函数 是减函数,且函数
是减函数,且函数 ,
, 满足不等式
满足不等式 .则当
.则当 时,
时, 的取值范围是( )
的取值范围是( )



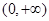 上的单调递减函数
上的单调递减函数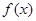 ,若
,若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )