题目内容
定义在 上的函数
上的函数 是减函数,且函数
是减函数,且函数 的图象关于原点成中心对称,若
的图象关于原点成中心对称,若 ,
, 满足不等式
满足不等式 .则当
.则当 时,
时, 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
D
解析试题分析:根据奇函数定义与减函数性质得出s与t的关系式,然后利用不等式的基本性质即可求得结果.解析:由f(x-1)的图象关于(1,0)中心对称知f(x)的图象关于(0,0)中心对称,故f(x)为奇函数得f(s2-2s) f(t2-2t),从而t2-2t
f(t2-2t),从而t2-2t s2-2s,化简得(t-s)(t+s-2)
s2-2s,化简得(t-s)(t+s-2) 0,又1
0,又1 s
s 4,故2-s
4,故2-s t
t s,从而
s,从而 ,而
,而 -1∈
-1∈ 故
故 的取值范围是
的取值范围是 ,选C.
,选C.
故选C.
考点:函数的奇偶性、单调性
点评:综合考查函数的奇偶性、单调性知识;同时考查由最大值、最小值求取值范围的策略,以及运算能力,属中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知函数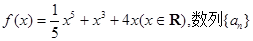 是等差数列,
是等差数列, 的值
的值
| A.恒为正数 | B.恒为负数 | C.恒为O | D.可正可负 |
定义域为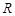 的奇函数
的奇函数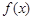 满足
满足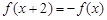 ,当
,当 时,
时,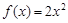 ,则
,则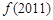 等于( )
等于( )
A.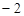 | B.0 | C.1 | D.2 |
定义在R上的偶函数 满足:对任意的
满足:对任意的 ,有
,有 .则( )
.则( )
A. | B.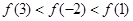 |
C. | D. |
 的图象如图,那么导函数
的图象如图,那么导函数 的图象可能是( )
的图象可能是( )

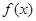 ,
,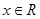 ,且
,且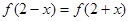 ,当
,当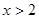 时,
时,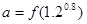 ,
,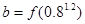 ,
,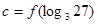 ,则
,则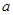 、
、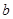 、
、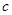 的大小顺序是( )。
的大小顺序是( )。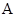 .
. 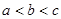
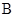 .
. 
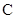 .
. 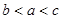
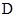 .
. 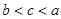
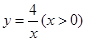 上,
上,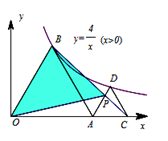
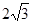 B.
B.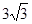 C.
C.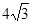 D.
D.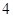
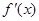 是函数
是函数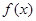 的导函数,将
的导函数,将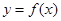 和
和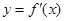 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )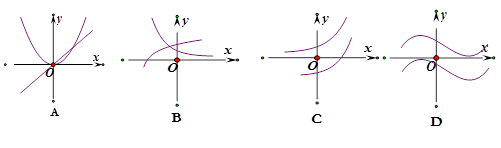
 的图象大致是
的图象大致是