题目内容
有两个分类变量X与Y,其观测值的2×2列联表如下: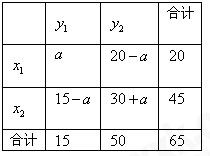
其中a,15-a均为大于5的整数,若K2≥2.706时,有90%的把握认为两个分类变量X与Y有关系,那么a为何值时,我们有90%的把握认为两个分类变量X与Y有关系?
分析:这是一个独立性检验应用题,处理本题的关键根据列联表,及K2的计算公式,计算出K2的值,并代入临界值表中进行比较,列出一个关于a的不等式组,解不等式组后,再根据a的取值范围,即可得到答案.
解答:解:计算K2=
=
=
由K2≥2.706得
(13a-60)2≥
≈1124.03
所以13a-60≥33.5或13a-60≤-33.5,
即a≥7.2或a≤2.
又a>5且15-a>5,
故5<a<10,
由于a为正整数,所以a=8或a=9
| 65×[a(30+a)-(15-a)(20-a)]2 |
| 15×50×45×20 |
=
| 13×(65a-300)2 |
| 50×45×60 |
| 13×(13a-60)2 |
| 90×60 |
由K2≥2.706得
(13a-60)2≥
| 270.6×54 |
| 13 |
所以13a-60≥33.5或13a-60≤-33.5,
即a≥7.2或a≤2.
又a>5且15-a>5,
故5<a<10,
由于a为正整数,所以a=8或a=9
点评:独立性检验,就是要把采集样本的数据,利用公式计算K2=
的值,比较与临界值的大小关系,来判定事件A与B是否无关的问题.具体步骤:(1)采集样本数据.(2)由K2=
计算的K2值.(3)统计推断,当K2>3.841时,有95%的把握说事件A与B有关;当K2>6.635时,有99%的把握说事件A与B有关;当K2≤3.841时,认为事件A与B是无关的.
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
