题目内容
在甲、乙两个盒子中分别装有标号为1、2、3、4、5、6的六个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
(III)求甲盒取出的球的标号大于乙盒取出的球的标号的概率.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
(III)求甲盒取出的球的标号大于乙盒取出的球的标号的概率.
分析:(I)先求出基本事件总数,然后记事件“取出两个球上标号为相邻整数”为事件A,列举出事件A所包含的基本事件,最后根据古典概型的概率公式解之即可;
(II)记事件“取出两个球上标号之和能被3整除”为事件B,列举出事件B所包含的基本事件,最后根据古典概型的概率公式解之即可;
(III)求出甲盒取出的球的标号等于乙盒取出的球的标号的基本事件的个数,即可得到结论.
(II)记事件“取出两个球上标号之和能被3整除”为事件B,列举出事件B所包含的基本事件,最后根据古典概型的概率公式解之即可;
(III)求出甲盒取出的球的标号等于乙盒取出的球的标号的基本事件的个数,即可得到结论.
解答:解:(I)基本事件总数为6×6=36种,
记事件“取出两个球上标号为相邻整数”为事件A,
事件包含(1,2),(2,1),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4),(5,6),(6,5),共10种
∴P(A)=
=
;
(II)记事件“取出两个球上标号之和能被3整除”为事件B,
事件包含(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),(3,3),(3,6),(6,3),(4,5),(5,4)共11种
∴P(B)=
;
(III)记事件“甲盒取出的球的标号大于乙盒取出的球的标号”为事件C
甲盒取出的球的标号等于乙盒取出的球的标号,共有基本事件6个
∴事件C包含的基本事件为
=15
∴P(C)=
.
记事件“取出两个球上标号为相邻整数”为事件A,
事件包含(1,2),(2,1),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4),(5,6),(6,5),共10种
∴P(A)=
| 10 |
| 36 |
| 5 |
| 18 |
(II)记事件“取出两个球上标号之和能被3整除”为事件B,
事件包含(1,2),(2,1),(1,5),(5,1),(2,4),(4,2),(3,3),(3,6),(6,3),(4,5),(5,4)共11种
∴P(B)=
| 11 |
| 36 |
(III)记事件“甲盒取出的球的标号大于乙盒取出的球的标号”为事件C
甲盒取出的球的标号等于乙盒取出的球的标号,共有基本事件6个
∴事件C包含的基本事件为
| 36-6 |
| 2 |
∴P(C)=
| 15 |
| 36 |
点评:本题主要考查了等可能事件的概率,解题的关键是弄清基本事件的个数与所求事件所包含的基本事件,属于中档题.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 的三个大小相同的球,现从甲、乙两个盒子中各取出
的三个大小相同的球,现从甲、乙两个盒子中各取出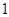 个球,每个球被取出的可能性相等.
个球,每个球被取出的可能性相等. 的概率.
的概率.