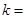题目内容
设函数 的定义域为(0,
的定义域为(0, ).
).
(Ⅰ)求函数 在
在 上的最小值;
上的最小值;
(Ⅱ)设函数 ,如果
,如果 ,且
,且 ,证明:
,证明: .
.
 的定义域为(0,
的定义域为(0, ).
).(Ⅰ)求函数
 在
在 上的最小值;
上的最小值;(Ⅱ)设函数
 ,如果
,如果 ,且
,且 ,证明:
,证明: .
.(Ⅰ) (Ⅱ)详见解析.
(Ⅱ)详见解析.
 (Ⅱ)详见解析.
(Ⅱ)详见解析.试题分析:(Ⅰ) 利用导数分析单调性,进而求最值;(Ⅱ)分类讨论函数的单调性
试题解析:(Ⅰ)
 ,则
,则 时,
时, ;
; 时,
时, 。
。所以,函数
 在(0,1)上是减函数,在(1,+
在(0,1)上是减函数,在(1,+ )上是增函数. 2分
)上是增函数. 2分当
 时,函数
时,函数 在[m,m+1]上是增函数,
在[m,m+1]上是增函数,此时
 ;
;当
 时,函数
时,函数 在[m, 1]上是减函数,在[1,m+1]上是增函数,
在[m, 1]上是减函数,在[1,m+1]上是增函数,此时
 ; 6分
; 6分(Ⅱ)证明:考察函数
 ,
,
所以g(x)在(
 )内是增函数,在(
)内是增函数,在( )内是减函数.(结论1)
)内是减函数.(结论1)考察函数F(x)=g(x)-g(2-x),即

于是

当x>1时,2x-2>0,从而

 (x)>0,
(x)>0,从而函数F(x)在[1,+∞)是增函数。
又F(1)=
 F(x)>F(1)=0,即g(x)>g(2-x). (结论2) 10分
F(x)>F(1)=0,即g(x)>g(2-x). (结论2) 10分若
 ,由结论1及
,由结论1及 ,得
,得 ,与
,与 矛盾;
矛盾;若
 ,由结论1及
,由结论1及 ,得
,得 ,与
,与 矛盾; 12分
矛盾; 12分若
 不妨设
不妨设
由结论2可知,g(
 )>g(2-
)>g(2- ),所以
),所以
 >g(2-
>g(2- )。
)。因为
 ,所以
,所以 ,又由结论1可知函数g(x)在区间(-∞,1)内是增函数,
,又由结论1可知函数g(x)在区间(-∞,1)内是增函数,所以
 >
> ,即
,即 >2. 15分
>2. 15分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
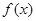 的单调区间;
的单调区间; 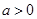 时,求函数
时,求函数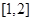 上的最小值.
上的最小值.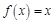 的
的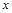 称为
称为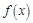 的一阶不动点,符合
的一阶不动点,符合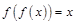 的
的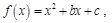 若函数
若函数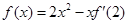 ,则函数
,则函数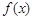 的图象在点
的图象在点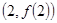 处的切线方程是 .
处的切线方程是 . 在点
在点 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,令
,令 ,则
,则 的值为___________.
的值为___________.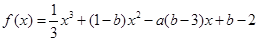 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是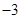 ,则不等式组
,则不等式组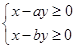 所确定的平面区域在
所确定的平面区域在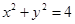 内的面积为 .
内的面积为 .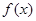 的定义域为R,
的定义域为R,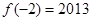 ,对任意
,对任意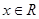 ,都有
,都有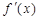 <
<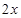 成立,则不等式
成立,则不等式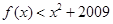 的解集为( )
的解集为( ) )
)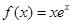 ,则
,则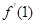 =
= 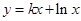 在点
在点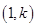 处的切线平行于
处的切线平行于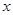 轴,则
轴,则