题目内容
用定义证明函数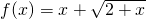 在其定义域上的单调性,并求函数在[2,7]上的最值.
在其定义域上的单调性,并求函数在[2,7]上的最值.
证明:函数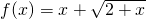 的定义域为[-2,+∞),…(2分)
的定义域为[-2,+∞),…(2分)
设任意x1,x2∈[-2,+∞),且x1<x2,则x1-x2<0,…(3分)
所以f(x1)-f(x2)=
 =
= =
= …(7分)
…(7分)
所以函数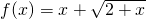 在其定义域上是增函数.…(8分)
在其定义域上是增函数.…(8分)
所以函数在[2,7]上的最大值为 ,…(10分)
,…(10分)
函数在[2,7]上的最小值为 .…(12分)
.…(12分)
分析:根据函数单调性的定义,首先在所给区间上任设两个数并规定大小,然后通过作差法分析获得两数对应函数值之间的大小关系即可;利用单调性,可求函数在[2,7]上的最值.
点评:本题考查的是函数单调性的判断和应用问题,解答的关键是作差法并化简.
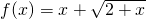 的定义域为[-2,+∞),…(2分)
的定义域为[-2,+∞),…(2分)设任意x1,x2∈[-2,+∞),且x1<x2,则x1-x2<0,…(3分)
所以f(x1)-f(x2)=

 =
= =
= …(7分)
…(7分)所以函数
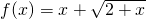 在其定义域上是增函数.…(8分)
在其定义域上是增函数.…(8分)所以函数在[2,7]上的最大值为
 ,…(10分)
,…(10分)函数在[2,7]上的最小值为
 .…(12分)
.…(12分)分析:根据函数单调性的定义,首先在所给区间上任设两个数并规定大小,然后通过作差法分析获得两数对应函数值之间的大小关系即可;利用单调性,可求函数在[2,7]上的最值.
点评:本题考查的是函数单调性的判断和应用问题,解答的关键是作差法并化简.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
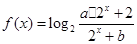 (
(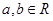 )的图象过点(1,2),它的反函数的图象也过点(1,2)。
)的图象过点(1,2),它的反函数的图象也过点(1,2)。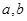 的值,并求函数
的值,并求函数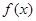 的定义域和值域;
的定义域和值域;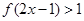 。
。