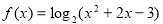题目内容
(1)求不等式的解集: .
.
(2)求函数的定义域: .
.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)首先将首项系数化为正数,然后分解因式,进而可求得不等式的解集;(2)首先根据根式要有意义建立不等式,然后通过解分式不等式可求得结果.
试题解析:(1)∵ ,∴
,∴ ,
,
∴ ,∴
,∴ 或
或 ,
,
∴原不等式的解集为 .
.
(2)要使函数 有意义,须
有意义,须 ,解得
,解得 或
或 ,
,
∴函数的定义域是 .
.
考点:1.一元二次不等式的解法;2.函数定义域.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目