Question

如下图,正方体ABCD—A₁B₁C₁D₁中,M,N,P分别是CC₁,B₁C₁,D₁C₁的中点.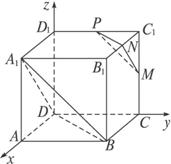

求证:(1)AP⊥MN;

(2)平面PMN∥平面A₁BD.

Answer 1

证明：（1）如图，建立空间直角坐标系，设正方体的棱长为1，

则A（1，0，0），P（0，，1），M（0，1，），N（，1，1）.

所以=(-1,,1),=(,0,).

所以·=（-1，，1）·（，0，）=0.

所以AP⊥MN.

(2)因为=(1,0,1),MN=(,0,),

所以∥,

即MN∥DA₁.

又因为=(,,0),=(1,1,0),

所以∥,即PN∥DB.

又因为PN∩MN=N,

所以平面PMN∥平面A₁BD.