题目内容
2. 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.(1)求异面直线DD1与MC1所成的角;
(2)求直线MC1与平面BB1C1C所成的角.
分析 (1)说明∠MC1C就是异面直线DD1 与MC1所成的角,连接MC,在△C1MC中求解即可.
(2)连接BC1,说明∠MC1B为直线MC1与平面BB1C1C所成的角,由△MC1B为Rt△.求解即可.
解答 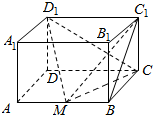 解:(1)因为C1C∥D1D,所以∠MC1C就是异面直线
解:(1)因为C1C∥D1D,所以∠MC1C就是异面直线
DD1 与MC1所成的角,…(3分)
连接MC,则△C1MC为Rt△.易得MC=$\sqrt{3}$,MC1=2,
所以∠MC1C=60○.
即异面直线DD1 与MC1所成的角为60°;…(6分)
(2)因为MB⊥平面B1C1CB,连接BC1,则∠MC1B为直线MC1与平面BB1C1C所成的角,…(9分)
由△MC1B为Rt△.易得BC1=$\sqrt{3}$,MC1=2,所以∠MC1B=30○,
即直线MC1与平面BB1C1C所成的角为30°;…(12分)
点评 本题考查直线与平面所成角,异面直线所成角的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
12.已知抛物线y=$\frac{1}{2}$x2的焦点与椭圆$\frac{y^2}{m}$+$\frac{x^2}{2}$=1的一个焦点重合,则m=( )
| A. | $\frac{7}{4}$ | B. | $\frac{127}{64}$ | C. | $\frac{9}{4}$ | D. | $\frac{129}{64}$ |
17.过点P(2,3),并且在两坐标轴上的截距相等的直线方程是( )
| A. | x-y+1=0 | B. | x-y+1=0或3x-2y=0 | ||
| C. | x+y-5=0 | D. | x+y-5=0或3x-2y=0 |
7.已知m、n表示两条不同的直线,α、β表示两个不同的平面,且m⊥α,n?β,则“α⊥β”是“m∥n”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
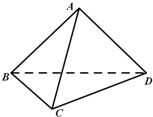 如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.
如图,在三棱锥A-BCD中,AB=AC,BC=CD,∠BCD=60°.