Question

1．已知变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$，则目标函数2x-y的最大值是7．

Answer 1

分析 利用线性规划的内容作出不等式组对应的平面区域，设z=2x-y，然后根据直线平移确定目标函数的最大值．

解答 解：作出不等式组对应的平面区域如图：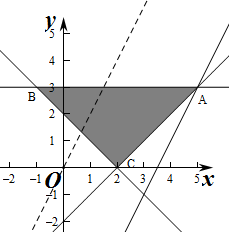
设z=2x-y得y=2x-z，平移直线y=2x-z，
由图象可知当直线经过点A时，直线在y轴的截距最小，此时z最大，
由$\left\{\begin{array}{l}{y=3}\\{x-y=2}\end{array}\right.$，得$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$，即A（5，3），
代入z=2x-y得最大值z=2×5-3=10-3=7．
故答案为：7．

点评 本题主要考查二元一次不等式组表示平面区域的知识，以及线性规划的基本应用，利用数形结合是解决此类问题的关键．