题目内容
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,决出胜负即停止比赛。按以往的比赛经验,每局比赛中,甲胜乙的概率为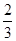 。
。
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设比赛的局数为X,求X的分布列和数学期望。
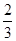 。
。(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设比赛的局数为X,求X的分布列和数学期望。
(1) ;
;
(2) ;
;
(3)X的分布列如下:
 。
。
 ;
;(2)
 ;
;(3)X的分布列如下:
| X | 3 | 4 | 5 |
| P |  |  |  |
 。
。本试题主要是考查了古典概型概率的运用,以及分布列和数学期望值的求解的综合运用。
(1)因为乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,决出胜负即停止比赛。按以往的比赛经验,每局比赛中,甲胜乙的概率为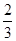 利用独立重复试验的概率值可以解得。
利用独立重复试验的概率值可以解得。
(2)根据已知题意得到X的可能取值为3,4,5,然后分别求解各个取值的概率值,得到结论。
(1)因为乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,决出胜负即停止比赛。按以往的比赛经验,每局比赛中,甲胜乙的概率为
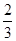 利用独立重复试验的概率值可以解得。
利用独立重复试验的概率值可以解得。(2)根据已知题意得到X的可能取值为3,4,5,然后分别求解各个取值的概率值,得到结论。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 局
局 胜制(即先胜
胜制(即先胜
















 C、
C、 D.、
D.、

 ,他连续测试3次,那么其中恰有1次获得通过的概率是( )
,他连续测试3次,那么其中恰有1次获得通过的概率是( )


